Solveeit Logo
Login

Question

Question: A point A(2, 1) is outside the circle \({{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\) and AP, AQ are the tangent...

A point A(2, 1) is outside the circle x2+y2+2gx+2fy+c=0{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 and AP, AQ are the tangents to the circle. The equation of the circle circumscribing the triangle APQ is:
(a) (x+g)(x-2)+(y+f)(y-1)=0
(b) (x+g)(x-2)-(y+f)(y-1)=0
(c) (x-g)(x+2)+(y-f)(y+1)=0
(d) (x-g)(x-2)+(y-f)(y-1)=0

Explanation

Solution

First, before proceeding for this, we must draw the following circle with all the conditions mentioned in the question to understand it easily. Then, from the figure, we can see clearly that we need to find the equation of the new circle formed whose diameter is OA. Then, by finding the slope of the two lines AO and OP, and by using the condition that two perpendicular lines slope when multiplied gives the value as -1, we get the final expression of the required circle.

Complete step by step answer:
In this question, we are supposed to find the equation of the circle circumscribing the triangle APQ when a point A(2, 1) is outside the circle x2+y2+2gx+2fy+c=0{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 and AP, AQ are the tangents to the circle.
So, before proceeding for this, we must draw the following circle with all the conditions mentioned in the question to understand it easily as:

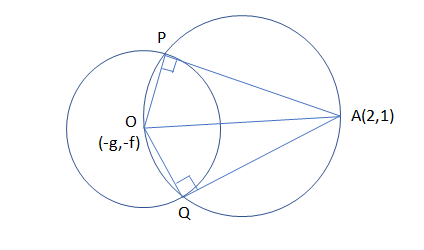
Now, let us assume the coordinates of P as (h, k) and then proceed further.
Then, from the figure, we can see clearly that we need to find the equation of the new circle formed whose diameter is OA.
So, by using the slope m1{{m}_{1}} of the line AP, we get:
m1=k−1h−2{{m}_{1}}=\dfrac{k-1}{h-2}
Similarly, we can find the slope m2{{m}_{2}}of the line OP, we get:
m2=k+fh+g{{m}_{2}}=\dfrac{k+f}{h+g}
Now, we know that two perpendicular lines slope when multiplied gives the value as -1.
So, we can see that lines AP and OP are perpendicular and by applying the same condition on them, we get:
m1×m2=−1{{m}_{1}}\times {{m}_{2}}=-1
Now, by substituting the value of m1{{m}_{1}}and m2{{m}_{2}} in the above expression, we get:
k−1h−2×k+fh+g=−1\dfrac{k-1}{h-2}\times \dfrac{k+f}{h+g}=-1
Then, by solving the above expression, we get:
(k−1)(k+f)=−(h−2)(h+g) ⇒(k−1)(k+f)+(h−2)(h+g)=0 \begin{aligned} & \left( k-1 \right)\left( k+f \right)=-\left( h-2 \right)\left( h+g \right) \\\ & \Rightarrow \left( k-1 \right)\left( k+f \right)+\left( h-2 \right)\left( h+g \right)=0 \\\ \end{aligned}
Now, to get the expression of the circle in coordinates form, we replace h by x and k by y, then we get:
(y−1)(y+f)+(x−2)(x+g)=0\left( y-1 \right)\left( y+f \right)+\left( x-2 \right)\left( x+g \right)=0
So, we get the equation of the circle as (x−2)(x+g)+(y−1)(y+f)=0\left( x-2 \right)\left( x+g \right)+\left( y-1 \right)\left( y+f \right)=0.

So, the correct answer is “Option A”.

Note: Now, to solve these types of questions we need to know some of the basics of the straight line equation beforehand to solve accurately. So, the equation of the straight line with slope m and points (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) is given by:
y−y1=m(x−x1)y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)