Question

A plumb line suspended from the roof of a carriage moving with acceleration ‘a’ incline at an angle $\theta$ with the vertical, then
A. $a = g\tan \theta$
B. $a = \dfrac{F}{m}$
C. $a = \dfrac{{dV}}{{dt}}$
D. $a = \dfrac{{{d^2}x}}{{d{t^2}}}$

Answer 1

The plumb line is attached to the roof of the moving carriage so the acceleration of both will be the same (a). There exists one more acceleration i.e. acceleration due to gravity (g). Find a relation relating a, g and $\theta$, you will get the final answer.

Complete step by step answer:
The above situation is depicted below.

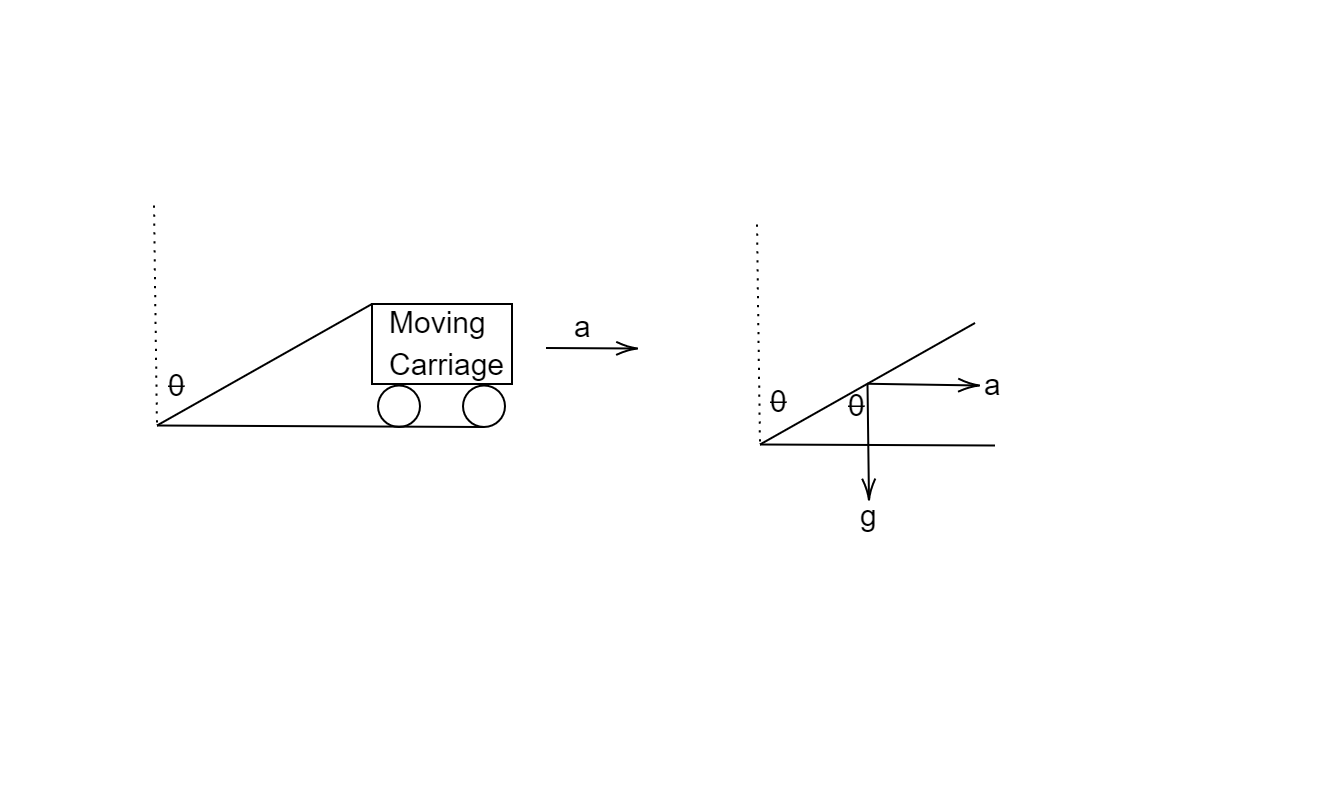
The plumb line is attached to the roof of the moving carriage so the acceleration of both will be the same (a). There exists one more acceleration i.e. acceleration due to gravity (g). By resolving the two acceleration in x and y direction we get the above picture.
The acceleration due to gravity is in negative y direction while acceleration of carriage is in positive x direction. By simple geometry, we get that the angle between acceleration due to gravity and plumb line is also $\theta$. Depicted in the figure in the right, we see from the triangle formed that,
$$
\tan \theta = \dfrac{{perpendicular}}{{base}} \\
\tan \theta = \dfrac{a}{g} \\

Therefore, we can express the value of given parameter a with the angle of plumb line makes with vertical: $$a = g\tan \theta $$ The correct answer is option A. **Additional information:** The question can also be given as, ‘Given a and g, find the angle made by the plumb line with the ground’. In this case, the same approach should be taken. Now, $$\theta = {\tan ^{ - 1}}\dfrac{a}{g}$$ But this is the angle with the vertical. For angle with ground, $\theta ' = \,{90^ \circ } - \theta $ **Note:** The acceleration of plumb line is along the same direction as the carriage i.e. along positive x-direction. Sometimes students make this mistake in that they assign the direction of acceleration of the plumb line along the plumb line i.e. along the direction at an angle $\theta $ with vertical. This is wrong and the correct concept should be clear.