Question

A plumb bob is hung from the ceiling of a train compartment. The train moves on an inclined track of inclination $30^\circ$ with horizontal acceleration of the train up the plane is $a = \dfrac{g}{2}$ . Find the angle which the string is supporting the bob makes with normal to the ceiling in equilibrium.

Answer 1

First of all, we will draw the free body diagram of the arrangement as mentioned in the question. Then we will equate the forces along the horizontal and the vertical direction. We will manipulate accordingly and obtain the result.

Step by step answer: In the given question, we are supplied with the following data:
A plumb bob is hung from the ceiling of the train compartment.
The train is moving on an inclined track, whose inclination is $30^\circ$ .
The acceleration of the train is half of the acceleration due to gravity i.e. $a = \dfrac{g}{2}$ .
We are asked to find the angle which the string that is supporting the bob, makes with the normal to the ceiling in equilibrium.

To begin with, we have to make a diagram of the train compartment along with the bob hanging from the ceiling, and show all the forces that are interfering in it. It is important to show all the forces, which are acting on the bob and the string. The bob actually oscillates as the train moves, such that it makes an angle of $\theta$ . The weight of the bob acts in a downward direction. The tension in the string acts in the upward direction along the string. The two components of the weight are also shown in the diagram. We will equate the forces which balance each other.

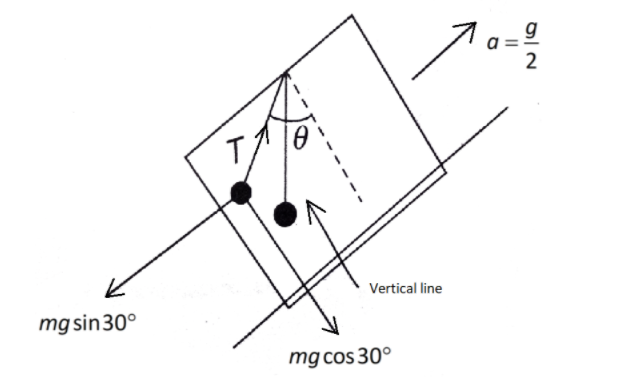
Now, we resolve the tension force:
The tension component along the plane is $T\sin \theta$ .
While the tension component along the normal in the upward direction is $T\cos \theta$ .
Now, we equate the forces:
Along the plane:
$T\sin \theta - mg\sin 30^\circ = ma$ …… (1)
Where,
$mg$ indicates the weight of the bob.
$a$ indicates the acceleration with which it is moving up the inclined plane.
Now, we substitute the required values in the equation (1) and we get:
$\Rightarrow T\sin\theta - mg\,sin30^\circ = ma$
$\Rightarrow T\sin\theta = m\times\,\dfrac{g}{2}+mg\sin\theta$
$\Rightarrow T\sin\theta = m\times\,\dfrac{g}{2}+mg\,times \dfrac{1}{2}$
$\Rightarrow T\sin \theta = mg$ …… (2)

Again, along the vertical:
$\Rightarrow T\cos \theta = mg\cos 30^\circ$
$\Rightarrow T\cos \theta = mg \times \dfrac{{\sqrt 3 }}{2}$ …… (3)

Now, we divide the equations (2) and (3):
$\Rightarrow \dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{mg}}{{mg \times \dfrac{{\sqrt 3 }}{2}}} \\\ \Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{{\dfrac{{\sqrt 3 }}{2}}} \\\ \Rightarrow \tan \theta = \dfrac{2}{{\sqrt 3 }} \\\ \Rightarrow \theta = {\tan ^{ - 1}}\left( {\dfrac{2}{{\sqrt 3 }}} \right) \\\$
Hence, the angle which the string that is supporting the bob, makes with the normal to the ceiling in equilibrium is ${\tan ^{ - 1}}\left( {\dfrac{2}{{\sqrt 3 }}} \right)$ .

Note: In order to solve problems in mechanics, we must always resolve all the forces which are actually acting on the objects. In such a case, if we miss out even one of the forces, then it will produce irrelevant results. Always remember that the tension force always acts in the upward direction along the string.