Question
Question: A plumb bob is hanging from the ceiling of a car. If the car moves with an acceleration \(a\), the a...
A plumb bob is hanging from the ceiling of a car. If the car moves with an acceleration a, the angle made by the string with the vertical is
A)tan−1(ga)B)tan−1(ag)C)cos−1(ga)D)cos−1(ag)
Solution
When the car starts moving, pseudo force acts on the plumb bob. This force will cause the plumb bob to move backwards, if the car is moving forward. Pseudo force is defined as the force that appears to be acting on a mass, whose motion is described using a non-inertial frame of reference.
Complete answer:
Pseudo force is defined as the force that appears to be acting on a mass, when the motion of mass is described in a non-inertial frame of reference. To understand this, let us take the example of a plumb bob, released from the ceiling of a car, as given in the question. We know that when the car starts moving forward, the plumb bob will move backwards, or the string attached to the plumb bob will get tilted towards the left, from its vertical position. The angle made between the tilted string and its vertical position is denoted as θ, as shown in the following diagram. Here, the non-inertial frame of reference is the accelerating frame of reference of the moving car. When we describe the motion of the plumb bob with respect to this accelerating frame of reference of the car, it appears to be acted upon by a force. This force is nothing but a pseudo force.
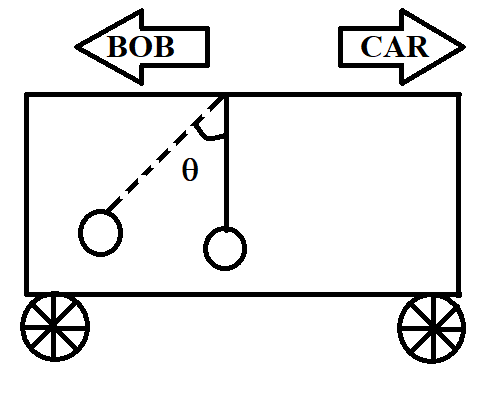
Coming to our problem, we are required to find the value of θ, which is the angle between the vertical position of the string and the tilted position of the string, as shown in the figure. At the tilted position, the bob experiences a force equal to the force with which the car is moving, but in the opposite direction. If ma is the force acting on the car, the force on the bob is also equal to ma, but in the opposite direction, as shown. At the same time, gravitational force too acts on the plumb bob. This gravitational force is equal to the weight of the plumb bob and is given by mg. The direction of gravitational force is downwards, as shown.
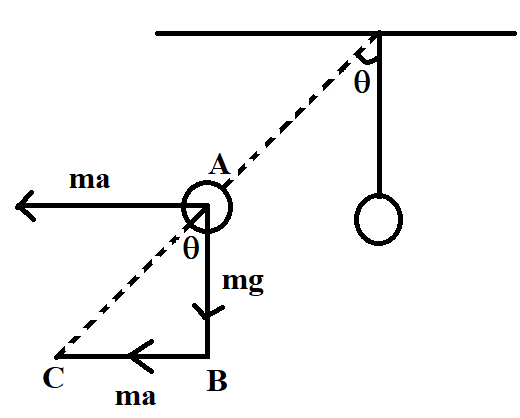
Now, if we draw a triangle connecting the tilted bob, the force acting on the bob and the gravitational force as shown, it is obvious that angle A of the right triangle ABC is equal to θ, due to the property of parallel lines. Now, we know that tanθ in a right triangle is the ratio of its opposite side to the base of the triangle. Therefore, in triangle ABC, tanθ is given by
tanθ=ABBC=mgma=ga
Taking θ outside, we have
θ=tan−1(ga)
Therefore, the angle made by the string with the vertical is tan−1(ga).
So, the correct answer is “Option A”.
Note:
Students need not get confused with the way tanθ is calculated in triangle ABC. In the above solution, we have equated the sides of the triangle with vectors ma and mg. Students need to understand that it is the ratio of these sides that is important and not the actual measurements of the sides, in order to determine the value of tanθ. Therefore, sides can be equated to the corresponding vectors, in the case of angle measurements.
