Question

A plot of volume (V) versus temperature (T) for a gas at constant pressure is a straight line passing through the origin. The plots at different values of pressure are shown in figure.

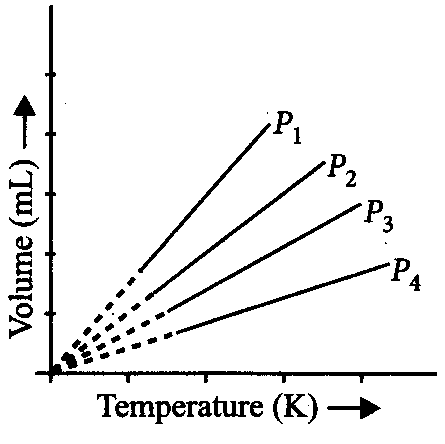
Which of the following order of pressure is correct for this gas?

• A.
• B. $\mathrm { P } _ { 1 } = \mathrm { P } _ { 2 } = \mathrm { P } _ { 3 } = \mathrm { P } _ { 4 }$
• C. $\mathrm { P } _ { 1 } < \mathrm { P } _ { 2 } < \mathrm { P } _ { 3 } < \mathrm { P } _ { 4 }$
• D. $\mathrm { P } _ { 1 } < \mathrm { P } _ { 2 } = \mathrm { P } _ { 3 } < \mathrm { P } _ { 4 }$

Answer 1

Answer: (C)

$\mathrm { P } _ { 1 } < \mathrm { P } _ { 2 } < \mathrm { P } _ { 3 } < \mathrm { P } _ { 4 }$

Answer 2

: PV = constant at given temperature

$\therefore \mathrm { P } _ { 1 } \mathrm {~V} _ { 1 } = \mathrm { P } _ { 2 } \mathrm {~V} _ { 2 } = \mathrm { P } _ { 3 } \mathrm {~V} _ { 3 } = \mathrm { P } _ { 4 } \mathrm {~V} _ { 4 }$

Now, $V _ { 1 } > V _ { 2 } > V _ { 3 } > V _ { 4 }$ (From the figures)

Hence, $\mathrm { P } _ { 1 } < \mathrm { P } _ { 2 } < \mathrm { P } _ { 3 } < \mathrm { P } _ { 4 }$ $\left( \because \mathrm { P } \propto \frac { 1 } { \mathrm {~V} } \right)$