Question

A platform is pulled with a constant acceleration a; A particle is projected from the platform at angle $\theta$ with the horizontal with respect to the platform as shown in the figure. The value of $\tan \theta$ is such that particle again come to the starting point on the platform is $\left( {a = 5m/{s^2}} \right)$ use $g = 10m/{s^2}$.

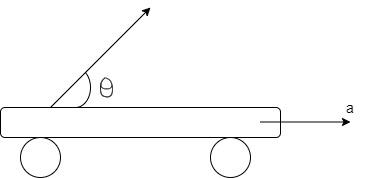
A) 4
B) 6
C) 2
D) 3

Answer 1

We have been given the acceleration due to gravity ‘g’ and horizontal acceleration ‘a’. One has to throw a particle while the platform is moving in such a way that the particle should again come to the starting point. Here. resolve the angle in the x and y direction and divide them together.

Complete step by step solution:
Here we need to make two equations one in x direction and another one in y direction.
The motion of particle in x direction:
${S_x} = 0$;
From the equations for kinematics:
${S_x} = u + \dfrac{1}{2}a{t^2}$;
Here:
${S_x}$= Distance in the x direction.
u = Initial velocity;
a = Acceleration;
t = time;
$\Rightarrow {S_x} = u\cos \theta - \dfrac{1}{2}g{t^2}$;
Write the above equation in terms of t:
$\Rightarrow u\cos \theta = \dfrac{1}{2}g{t^2}$;
$\Rightarrow \dfrac{{2u\cos \theta }}{g} = {t^2}$;
Similarly, in the y direction,
${S_y} = 0$;
${S_y} = u + \dfrac{1}{2}a{t^2}$;
$\Rightarrow {S_y} = u\sin \theta - \dfrac{1}{2}g{t^2}$;
Write the above equation in terms of t:
$\Rightarrow u\sin \theta = \dfrac{1}{2}g{t^2}$;
$\Rightarrow \dfrac{{2u\sin \theta }}{g} = {t^2}$;
Now, divide $\dfrac{{2u\sin \theta }}{g} = {t^2}$by $\dfrac{{2u\cos \theta }}{g} = {t^2}$:
$\Rightarrow \dfrac{{2u\sin \theta }}{g} \times \dfrac{g}{{2u\cos \theta }} = \dfrac{{{t^2}}}{{{t^2}}}$ ;
Cancel out the common factors:
$\Rightarrow \dfrac{{\sin \theta }}{1} \times \dfrac{1}{{\cos \theta }} = 1$;
Solve the above equation:
$\Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = 1$;
$\Rightarrow \tan \theta = 1$;
We know that $\tan \theta$ is equal to perpendicular upon base:
$\Rightarrow \tan \theta = \dfrac{g}{a}$;
Put in the given value in the above equation:
$\Rightarrow \tan \theta = \dfrac{{10}}{5}$;
$\Rightarrow \tan \theta = 2;$

Final Answer: Option “C”. The value of $\tan \theta$ is such that particles again come to the starting point on the platform is 2.

Note: We have to apply the equations of kinematics for both x and y axis as the particle would be projected in x and y direction. Here, one has to go step by step. First write the equation in the x direction and then write the equation in the y direction and then solve both equations by dividing each other.