Solveeit Logo
Login

Question

Question: A plastic rod of length \(1.0{\text{ }}m\)carries uniform positive charge \( + 4{\text{ }}\mu C\) on...

A plastic rod of length 1.0 m1.0{\text{ }}mcarries uniform positive charge +4 μC + 4{\text{ }}\mu C on half of its length and uniform negative charge −4 μC - 4{\text{ }}\mu C on the remaining half of its length. Find the magnitude of its net dipole moment in μC−m\mu C - m.

Explanation

Solution

A configuration of two charges of equal magnitude but opposite direction separated at a small distance is known as dipole. In the given every value of the variable is given. Hence, we will just use the formula of dipole moment to find the answer.

Formula used:
p=q×2lp = q \times 2l
The variables are-
p=p = dipole moment
q=q = magnitude of charge
2l=2l = separation of charges.

Complete step-by-step solution:
A system of two charges of equal magnitude but different direction at a small distance is known as dipole.
Dipole moment is defined as the product of either charge and the distance of separation between both the charges.
So the formula is,
p=q×2l−−−−(1)p = q \times 2l - - - - \left( 1 \right)
The variables are-
p=p = dipole moment
q=q = magnitude of charge
2l=2l = separation of charges.

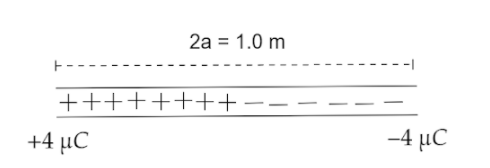
The values given in the question are-
q=4 μCq = 4{\text{ }}\mu C, 2l=1 m2l = 1{\text{ }}m
Substituting the values in equation (1)\left( 1 \right) we get,
p=4×1=4p = 4 \times 1 = 4
So, the dipole moment is 4 μC−m4{\text{ }}\mu C - m.

Additional information:
The electric potential due to an electric dipole at any given point is given by the formula,
V=14πεpcos⁡θ(r2−a2cos⁡2θ)V = \dfrac{1}{{4\pi \varepsilon }}\dfrac{{p\cos \theta }}{{\left( {{r^2} - {a^2}{{\cos }^2}\theta } \right)}} where, V=V = potential, r=r = distance of the point whose potential is to be found from the center of the dipole, a=a = half of the separation of charges in a dipole and θ=\theta = the angle between dipole axis and the point for which potential is to be found.

Note: The direction of dipole moment is from negative charge to positive charge. The dipole moment is generally a vector quantity but as the question has not assigned any direction, there is no need to mention that. The force experienced by a dipole in a uniform electric field is 00.