Question

A plastic ball falling from a height of 4.9 m rebounds a number of times. If the total time for the second collision is 2.4 s, then the coefficient of restitution is?

Answer 1

In this question we will use different expressions of time, velocity and the restitution coefficient. Also, by substituting the given values in the question, we will get the required restitution coefficient of the plastic ball. Further we will discuss the basics of collision and law of conservation of mass.
Formula used:
$t = \sqrt {\dfrac{{2H}}{g}}$
$v = \sqrt {2gH}$
$t = \dfrac{v}{g} = e\sqrt {\dfrac{{2H}}{g}}$

Complete step by step solution:
The total time for the second collision will be given as the time to fall down from the given height H in addition to the time it takes to rise and fall after the second collision.

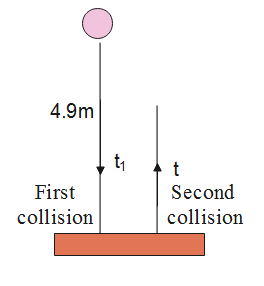
Now, as we know that relation between the time t and acceleration due to gravity g is given by:
$t = \sqrt {\dfrac{{2H}}{g}}$
Also, the velocity of the ball just before the first collision is given by:
$v = \sqrt {2gH}$
Now, after the first collision the velocity of ball becomes:
${v_1} = ev = e\sqrt {2gH}$
Here, e is the coefficient of restitution
The time of ascent is given as the time of decent as:
${t_1} = \dfrac{{{v_1}}}{g} = e\sqrt {\dfrac{{2H}}{g}}$
From this, the time for the second collision T will be give as:
$t + 2{t_1} = (1 + 2e)\sqrt {\dfrac{{2H}}{g}}$
By substituting the given values in above equation, we get:
\eqalign{ & 1 + 2e = 2.4 \cr & \therefore e = 0.7 \cr}
Therefore, we get the required value of coefficient of restitution e of plastic balls falling from a given height.

Additional information: As we know that when an object or particle is at a certain height, it gains potential energy.
Further, as we know that energy is defined as the ability to do work. As we know energy can be found in many different things and it can take different forms, like-kinetic energy is the energy of motion, and potential energy is the energy due to an object's position or structure.
Also, according to the law of conservation of mass, we know that mass can neither be created nor be destroyed in any chemical reactions.
We know that collision means when two objects come in contact with each other for a very short period. Collision is defined as the interaction between two masses for a very short duration. Here, the momentum and energy of the colliding masses changes. Also, there are two types of collision, first is elastic collision where the energy remains the same after interaction or collision and the second one is inelastic collision where the final energy of the object changes after the collision.

Note: Here, we should remember that time of flight can be measured for waves as well. During the solution, one should see that laws of conservation are not violated, i.e., mass can neither be created nor be destroyed and similarly for energy of the particles as well. Also, when an object is at the maximum height, then the potential energy is maximum and kinetic energy is zero.