Question

A plano-convex lens has thickness 4 cm. When placed on a horizontal table with the curved surface in contact with it, the apparent depth of the bottom-most point of the lens is found to be 3 cm. If the lens is inverted such that the plane face is in contact with the table, the apparent depth of the centre of the plane face of the lens is found to be 25/8 cm. Find the focal length of the lens?

Answer 1

Here we have to consider a refractive index which is denoted by μ, it is stated that is a value calculated from the ratio of the speed of light in a vacuum to that in a second medium of greater density. In simple words the refractive index determines how much the path of light is bent or we can say refracted when entering a material.

Formula used:
$\dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{{{R_1}}}$

Complete Step by step solution:

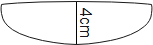
According to the question , when the curved surface of the lens refractive index μ is in contact with the table the image of the bottom most point of the lens is formed due to refraction at the plane face. The image of O appears at ${I_1}$ .

Now we take
\eqalign{ & {u_1} = AO = - 4cm \cr & {v_1} = A{I_1} = 3cm \cr}
${\mu _1} = \mu$ and ${\mu _2} = 1$ and ${R_1} = \infty$

Hence , substituting above values in the formula.
\eqalign{ & \dfrac{{{\mu _2}}}{v} - \dfrac{{{\mu _1}}}{u} = \dfrac{{{\mu _2} - {\mu _1}}}{{{R_1}}} \cr & \Rightarrow \dfrac{1}{{ - 3}} - \dfrac{\mu }{{ - 4}} = \dfrac{{1 - \mu }}{\infty } - - - - - - \left( 1 \right) \cr}

If the plane surface of the lens in contact with the table, the image of center of the plane face is formed due to refraction at curved surface, Then the image of O is formed at ${I_2}$ .
Here, u = AO = -4cm
$V = A{I_2} = \dfrac{{ - 25}}{8}$
\eqalign{ & {\mu _1} = \mu ,{\mu _2} = 1,and{R_2} = - R \cr & \therefore \dfrac{{{\mu _2}}}{{{V_2}}} - \dfrac{{{\mu _1}}}{{{\mu _2}}} = \dfrac{{{\mu _2} - {\mu _1}}}{{{R_2}}} \cr}

By substituting given values we have
$\dfrac{1}{{\left( {\dfrac{{ - 25}}{8}} \right)}} - \dfrac{u}{{ - 4}} = \dfrac{{1 - u}}{R}$

From equation (1) $\mu = \dfrac{4}{3}$ therefore this equation gives
\eqalign{ & \dfrac{{ - 8}}{{25}} + \dfrac{{\dfrac{4}{3}}}{4} = - \dfrac{{\left( {1 - \dfrac{4}{3}} \right)}}{R} \cr & \Rightarrow \dfrac{{ - 8}}{{25}} + \dfrac{1}{3} = \dfrac{1}{{3R}} \cr & \therefore \dfrac{1}{{75}} = \dfrac{1}{{3R}} \cr}
Therefore we have R= 25cm

For focal length of plano convex lense we take
${R_1} - R\& {R_2} = \infty$
\eqalign{ & \dfrac{1}{f} = \left( {\mu - 1} \right)\left( {\dfrac{1}{R} - \dfrac{1}{\infty }} \right) \cr & \Rightarrow \dfrac{1}{f} = \dfrac{{\left( {\mu - 1} \right)}}{R} = \dfrac{{\dfrac{4}{3} - 1}}{{25}} \cr & \Rightarrow \dfrac{1}{f} = \dfrac{1}{{75}} \cr & \therefore f = 75cm \cr}

Hence the focal length of the lense is 75cm.

Note:
Here we need to know a lens with more bending power has a shorter focal length because it alters the path of the light rays more effectively than a weaker lens. For thicker lenses we can say how thick they are does make a difference and in general its results in a shorter focal length.