Question

A Plano convex lens has a thickness of 4cm. When placed on the horizontal table, with the curved surface in contact with it, the apparent depth of the bottom most part of the lens is found to be 3cm. If the lens is inverted so that the plane face is in contact with the table the apparent depth is found to be $\dfrac{25}{8}$ cm. The focal length of the lens is
a) 75cm
b) 50cm
c) 60cm
d) 45cm

Answer 1

When the curved surface is in contact with the table of the les the refraction is observed from the flat surface. Similarly when the flat surface is in contact with the table the refraction is observed from the curved surface of the Plano convex lens. Hence from the respective refraction we need to obtain the radius of curvature of the lens and then from the lens makers formula we can obtain the focal length of the lens.
Formula used:
$\mu =\dfrac{{{D}_{R}}}{{{D}_{A}}}$
$\dfrac{{{\mu }_{1}}}{v}-\dfrac{{{\mu }_{2}}}{u}=\dfrac{{{\mu }_{1}}-{{\mu }_{2}}}{R}$
$\dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$

Complete step by step answer:
Let us say there is a biconcave lens with refractive index$\mu$ and with radius of curvature ${{R}_{1}}$ and ${{R}_{2}}$ . Than from the lens makers formula the focal length ‘f’ is given by,
$\dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$
For a Plano convex lens ${{R}_{2}}=0$
Hence the focal length of Plano convex lens is given by,
$\dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{R} \right]$

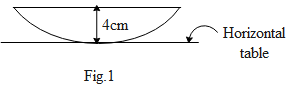
In the first case (as shown in the fig.1) the curved surface in contact with the horizontal table. Hence the refraction occurs at the plane surface. If ${{D}_{R}}$ is the depth of the point in contact with the table from the plane surface and ${{D}_{A}}$ is the apparent depth of the point, than the refractive index of the lens is given by,
$\begin{aligned} & \mu =\dfrac{{{D}_{R}}}{{{D}_{A}}}, \\\ & \because {{D}_{A}}=3cm,\text{ }{{D}_{R}}=4cm \\\ & \therefore \mu =\dfrac{4}{3} \\\ \end{aligned}$

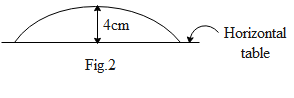
When the plane surface is in contact with the table(as shown in the fig.2), the refraction occurs at the curved surface.
If the refraction occurs from a denser to rarer medium of refractive indices ${{\mu }_{2}}$ and ${{\mu }_{1}}$, then the relation between the image distance ‘v’, the object distance ‘u’ and the radius of curvature of the Plano convex lens ‘R’ is given by,
$\dfrac{{{\mu }_{1}}}{v}-\dfrac{{{\mu }_{2}}}{u}=\dfrac{{{\mu }_{1}}-{{\mu }_{2}}}{R}$
For air ${{\mu }_{1}}=1$ , hence
$\dfrac{1}{v}-\dfrac{{{\mu }_{2}}}{u}=\dfrac{1-{{\mu }_{2}}}{R}$
The bottom most part of the lens is at a distance of 4cm from the top and the image formed of this is at a distance of $\dfrac{25}{8}$ cm. Therefore the radius of curvature R of the lens is,
$\begin{aligned} & \dfrac{1}{-25/8cm}-\dfrac{4/3}{-4cm}=\dfrac{4/3-1}{R} \\\ & \Rightarrow \dfrac{-8}{25cm}+\dfrac{1}{3cm}=\dfrac{1}{3R} \\\ & \Rightarrow \dfrac{1}{75cm}=\dfrac{1}{3R} \\\ & \therefore R=25cm \\\ \end{aligned}$
Therefore from the lens makers formula for Plano convex lens we get,
$\begin{aligned} & \dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{R} \right] \\\ & \Rightarrow \dfrac{1}{f}=(\dfrac{4}{3}-1)\left[ \dfrac{1}{25cm} \right] \\\ & \Rightarrow \dfrac{1}{f}=\dfrac{1}{3}\left[ \dfrac{1}{25cm} \right] \\\ & \therefore f=75cm \\\ \end{aligned}$
So, the correct answer is “Option a”.

Note: The image and the object distances are considered to be negative considering the direction of the incident rays. It is also to be noted that the radius of curvature of a Plano convex lens can be any one of the two as that of a biconcave lens.