Question

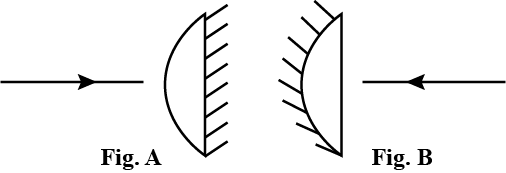
A plano-convex lens becomes an optical system of 28cm focal length when its plane surface is silvered and illuminated from left to right as shown in Fig-A.
If the same lens is instead silvered on the curved surface and illuminated from the other side as in Fig. B, it acts as an optical system of focal length 10 cm. The refractive index of the material of lens if:

Answer 1

A plano convex lens is given and needs to find the refractive index of material. It is easy to solve as formula for refractive index is $\dfrac{1}{f} = \left( {\mu - 1} \right)\dfrac{1}{R}$ where, $f$ is the focal length $\mu$ is refractive index and $R$ is radius of curvature. We will find total focal length for both the figure and also the radius of curvature through $B$ because focal length in figure $A$ is infinite.

Complete Step by Step Answer:
Step 1:
Refractive index, also called index of refraction, measures the bending of a ray of light when passing from one medium into another. Refractive index is also equal to the velocity of light $c$ of a given wavelength in empty space divided by its velocity $v$ in a substance, or $n=\dfrac{c}{v}$
The formula for refractive index is $\dfrac{1}{f} = \left( {\mu - 1} \right)\dfrac{1}{R}$
We are give a plano convex lens becomes an optical system of 28cm focal length when its plane surface is silvered and illuminated from left to right in figure $A$
Let the focal length of the convex lens be $F$. The convex lens then cut into half pieces then their focal length will also become half
Let focal length of convex part is ${f_1}$ =$\dfrac{f}{2}$ ….. (1)
And focal length of the plane part is ${f_m}$ (focal length for plane part will be infinite because of silver coating)……….. (2)
The total focal length is given as $28cm$
Solving for ${f_1}$,
$\dfrac{1}{F}$ =$\dfrac{1}{{{f_1}}}$ +$\dfrac{1}{\infty }$ (using 2)
Now substituting the value of $F=28$ and ${f_1}$ =$\dfrac{f}{2}$ we will get ${f_1}$ =56cm
Step 2:
Focal length for plane part in figure $B$ is ${f_m}$=$\dfrac{R}{2}$ (focal length is half of radius of curvature $R$ in plane)
Again applying the formula for total focal length for figure $B$
$\dfrac{1}{F}$ =$\dfrac{1}{{{f_1}}}$ +$\dfrac{1}{{{f_m}}}$
We have $F$ for figure $B$ is $10 cm$ and ${f_1} =56cm$ from here we will find $R$
Substituting the value
$\dfrac{1}{{10}}$ =$\dfrac{2}{{56}}$ +$\dfrac{2}{R}$
From here we will get $R$ equal to $31.1 cm$
Now we can calculate refractive index,
The formula for refractive index is $\dfrac{1}{f} = \left( {\mu - 1} \right)\dfrac{1}{R}$
Substituting the value of $f$ and $R$ we will get
$\Rightarrow$ $\dfrac{1}{{56}} = \left( {\mu - 1} \right)\dfrac{1}{{31.1}}$,
On solving we get
$\mu = 1.55$

$\therefore$ The refractive index of the material of lens is $\mu = 1.55$.

Note:
The focal length of a lens depends on the radii of curvature of its surfaces and on the index of refraction of the material the lens is made from. Higher angles of curvature lead to shorter focal lengths due to the fact that light waves are refracted at a greater angle with respect to the optical axis of the lens.