Question
Question: A plank P is placed on a solid cylinder S, which rolls on a horizontal surface. The two are of equal...
A plank P is placed on a solid cylinder S, which rolls on a horizontal surface. The two are of equal mass. There is no slipping at any surface in contact. The ratio of the kinetic energy of P to the kinetic energy of S is
A) 1:1
B) 2:1
C) 8:3
D) 11:8
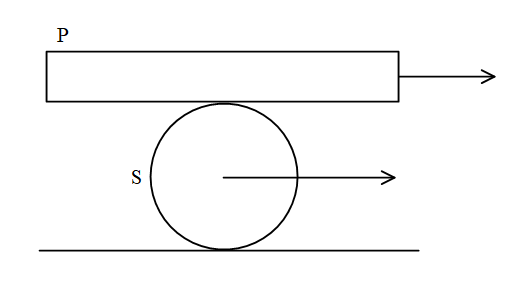
Solution
The point of contact of the plank and the solid cylinder has a velocity equal to the product of angular velocity and the distance from the center. There is no relative motion between the cylinder and the ground.
Complete step by step answer:
As it is given that the mass of the cylinder and mass of the plank is equal. The velocity of the plank is given by,
⇒vp=vs+ω⋅R………eq. (1)
As at the point of contact of the cylinder and the plank there is no relative motion therefore,
⇒vs−ω⋅R=0
⇒vs=ω⋅R………eq.(2)
Replace the value of ω⋅R is from the equation (2) into the equation (1).
⇒vp=vs+ω⋅R
⇒vp=vs+vs
⇒vp=2vs
Now let us calculate the kinetic energy of the plank and the solid cylinder respectively.
The kinetic energy of plank is given by,
⇒K.E=21⋅mp⋅v2p
⇒K.E=21⋅m⋅v2p
As vp=2vs
Therefore,
⇒K.E=21⋅m⋅(2vs)2
⇒K.E=4⋅21⋅m⋅v2s
⇒K.E=2⋅m⋅v2s………eq. (3)
And the kinetic energy of the solid is given by,
⇒K.E=21⋅ms⋅v2s+21Iω2
⇒K.E=21⋅ms⋅v2s+21Iω2
The moment of inertia is equal to I=2mR2 let us replace the value of the moment of inertia in the above relation to find the kinetic energy of plank P.
⇒K.E=21⋅ms⋅v2s+21Iω2
⇒K.E=21⋅m⋅v2s+21⋅(2mR2)ω2
On simplification,
⇒K.E=21⋅m⋅v2s+2m⋅(2ω2R2)
⇒K.E=21⋅m⋅v2s+2m⋅(2v2s)
On further calculations,
⇒K.E=2m⋅v2s+4m⋅v2s
⇒K.E=42m⋅v2s+m⋅v2s
⇒K.E=43m⋅v2s………eq. (4)
The ratio of the kinetic energy of the plank to the kinetic energy of the solid cylinder (from equation (3) and (4) )is equal to,
⇒(K.E)S(K.E)P=(43)⋅mvs22mvs2
⇒(K.E)S(K.E)P=(43)⋅mvs22mvs2
On cancelling the common terms,
⇒(K.E)S(K.E)P=38
Therefore, the ratio of the kinetic energy of the plank and the kinetic energy of the solid cylinder is equal to (K.E)S(K.E)P=38. The correct answer for this problem is option C.
Note:
The kinetic energy of a rotation body includes the moment of inertia of the rotating body. So students are advised to remember the moment of inertia of all the standard solids. There is no relative motion between the cylinder and the ground.
