Question

A plank of thickness ‘x’ can just stop a bullet, moving at a speed of $\sqrt 3 {\text{m}}{{\text{s}}^{ - 1}}$. Find the speed of the bullet that can be just stopped by a plank of thickness ${\text{3x}}$.
A) ${\text{3m}}{{\text{s}}^{ - 1}}$
B) ${\text{6m}}{{\text{s}}^{ - 1}}$
C) $\sqrt 3 {\text{m}}{{\text{s}}^{ - 1}}$
D) ${\text{9m}}{{\text{s}}^{ - 1}}$

Answer 1

When a bullet strikes a plank it moves through a distance equal to the thickness of the plank before coming to a stop. So the thickness of the plank will be the displacement of the bullet. Newton’s third equation of motion relating the final velocity, initial velocity, displacement and acceleration of a body can be used to obtain the required speed of the bullet.

Formula used:
Newton’s third equation of motion is given by, ${v^2} - {u^2} = 2as$ where $v$ is the final velocity of a body, $u$ is its initial velocity, $s$ is its displacement and $a$ is the acceleration of the body.

Complete step by step answer:
Step 1: Listing the parameters given in the question.
A bullet moving with some speed strikes a plank of some thickness and comes to a halt. This is sketched in the figure below.

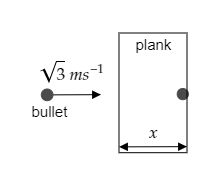
The thickness of the plank is the displacement of the bullet and it is given to be $s = x$ .
The initial velocity of the bullet is given to be $u = \sqrt 3 {\text{m}}{{\text{s}}^{ - 1}}$ .
The final velocity of the bullet will be zero. i.e., $v = 0$ .
Let $a$ be the acceleration of the bullet.
Step 2: Using Newton’s third equation of motion, obtain the acceleration of the bullet.
Newton’s third equation of motion is given by, ${v^2} - {u^2} = 2as$ .
$\Rightarrow a = \dfrac{{{v^2} - {u^2}}}{{2s}}$ -------- (1)
Substituting for $u = \sqrt 3 {\text{m}}{{\text{s}}^{ - 1}}$ , $v = 0$ and $s = x$ in equation (1) we get, $a = \dfrac{{{0^2} - {{\left( {\sqrt 3 } \right)}^2}}}{{2x}} = - \left( {\dfrac{3}{{2x}}} \right){\text{m}}{{\text{s}}^{ - 2}}$
Thus the acceleration of the bullet is $a = - \left( {\dfrac{3}{{2x}}} \right){\text{m}}{{\text{s}}^{ - 2}}$ .
Step 3: Again using Newton’s third equation of motion obtain the initial velocity of the bullet for the new displacement.
The new displacement of the bullet before coming to a stop is given to be $s = 3x$.
Then Newton’s third equation of motion gives ${v^2} - {u^2} = 2as$.
$\Rightarrow {u^2} = {v^2} - 2as$ ------- (2)
Substituting for $s = 3x$ , $v = 0$ and $a = - \left( {\dfrac{3}{{2x}}} \right){\text{m}}{{\text{s}}^{ - 2}}$ in equation (2) we get, ${u^2} = 0 + \left( {2 \times \dfrac{3}{{2x}} \times 3x} \right) = 9$
$\Rightarrow u = \sqrt 9 = 3{\text{m}}{{\text{s}}^{ - 1}}$
Thus the initial velocity of the bullet so that it is just stopped by the plank of thickness ${\text{3x}}$ is $u = 3{\text{m}}{{\text{s}}^{ - 1}}$.

Hence, the correct option is A.

Note:
The obtained acceleration of the bullet has a negative sign, $a = - \left( {\dfrac{3}{{2x}}} \right){\text{m}}{{\text{s}}^{ - 2}}$. This is because on striking the plank the velocity of the bullet decreases and becomes zero as the bullet comes to rest. So the acceleration of the bullet is, in fact, its retardation i.e., negative acceleration. For both planks, the acceleration of the bullet will be the same. We use Newton’s third equation of motion because it is the only equation which does not involve the time taken for the displacement.