Question

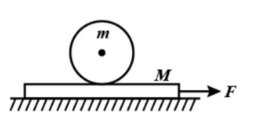
A plank of mass $M$ is placed on a smooth surface over which a cylinder of mass $m$ $(=M)$ and radius $R=1m$ is placed as shown in figure. Now the plank is pulled towards the right with an external force $F(=2MG)$. If the cylinder does not slip over the surface of the plank, then:
(Take$g=10\dfrac{m}{{{s}^{2}}}$)

A.)Linear acceleration of the plank is $5\dfrac{m}{{{s}^{2}}}$
B.)Linear acceleration of the cylinder is $10\dfrac{m}{{{s}^{2}}}$
C.)Angular acceleration of the cylinder is $10\dfrac{rad}{{{s}^{2}}}$
D.)Angular acceleration of the cylinder is $5\dfrac{rad}{{{s}^{2}}}$

Answer 1

Hint: When a rolling body does not slip over another body, it is the case of pure rolling. We will consider the presence of pseudo force on one object.

Complete step by step answer:

Plank of mass M is placed on a smooth surface and cylinder is placed on it. We are given that the cylinder does not slip over the surface of the plank; it means that the cylinder is undergoing pure rolling motion. We can also see friction on the cylinder in any direction, left or right. We will apply friction on the right side of the cylinder.
As the friction is acting on the cylinder towards the right direction, it must be acting towards the left direction on the plank to balance the forces.
Let the acceleration be ${{a}_{1}}$ by which plank is moving in the right direction. Due to the movement of the plank in the right direction, the cylinder will experience a pseudo force in the left direction.

Value of pseudo force $=m{{a}_{1}}$

Due to the result of pseudo force, the cylinder will move in the left direction with respect to the plank with acceleration, say ${{a}_{2}}$.

Let the angular acceleration of cylinder be $\alpha$

Using the equation of rolling motion, we get ${{a}_{2}}=R\alpha$ where $R$ is the radius of the cylinder.

For translation motion of plank, $F-f=M{{a}_{1}}$ where $f$ is the force of friction on plank.

For translation motion of cylinder, $m{{a}_{1}}-f=m{{a}_{2}}$

Rotational motion of cylinder with respect to the plank $fR=I\alpha$

Value of moment of inertia $I=\dfrac{1}{2}m{{R}^{2}}$ and $\alpha =\dfrac{{{a}_{2}}}{R}$

Also, $f=\dfrac{1}{2}m{{a}_{2}}$

Solving above equations,

$\begin{aligned} & m{{a}_{1}}-\dfrac{1}{2}m{{a}_{2}}=m{{a}_{2}} \\\ & {{a}_{1}}=\dfrac{3}{2}{{a}_{2}} \\\ \end{aligned}$

And,

$\begin{aligned} & F-\dfrac{1}{2}m{{a}_{2}}=\dfrac{3}{2}M{{a}_{2}} \\\ & {{a}_{2}}=\dfrac{2F}{3M+m} \\\ \end{aligned}$

Putting values in above equation,

$\begin{aligned} & {{a}_{2}}=10\dfrac{m}{{{s}^{2}}} \\\ & {{a}_{1}}=15\dfrac{m}{{{s}^{2}}} \\\ \end{aligned}$

Net acceleration of the cylinder relative to the plank will be given by ${{a}_{1}}-{{a}_{2}}$
Acceleration of the cylinder

${{a}_{\text{cylinder}}}={{a}_{1}}-{{a}_{2}}=15-10=5\dfrac{m}{{{s}^{2}}}$

Angular acceleration of cylinder $\alpha =\dfrac{{{a}_{2}}}{R}=10\dfrac{rad}{{{s}^{2}}}$
Hence, correct options are B and C.

Note:
Pseudo force is very necessary to be taken into consideration when the frame of reference has started accelerating compared to a non-accelerating frame. This is not a real force but arises due to the acceleration of the non-inertial frame.