Question
Question: A plank of mass \(m\) and length \(L\) is placed on a table such that \(\dfrac{L}{3}\) length is out...
A plank of mass m and length L is placed on a table such that 3L length is out of the table. A person of mass 2m is standing on the plank such that his position is at the edge of the table. Find the distance on plank which the person can move such that the plank does not fall (figure)
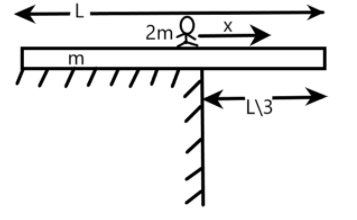
A)X=6LB)X=12LC)X=18L
D)None of these
Solution
The net torque acting at a point is equal to zero, when two masses are balanced on either side of the point. Edge of the table is considered as the balancing point of the plank. For the plank to balance at this point, torque on the left side of the plank about the edge of the table is equal to the torque on the right side of the plank about the edge of the table.
Formula used:
1)τedge=0⇒τleft=τright
2)τleft=m×(L−3L)
3)τright=2mx
Complete answer:
We are given a plank of mass m and length L, placed on a table such that 3L of its length is out of the table, as shown in the following figure. A person of mass 2m is standing on the plank such that his position is at the edge of the table. We are required to find the distance on the plank which the person can move such that the plank does not fall.
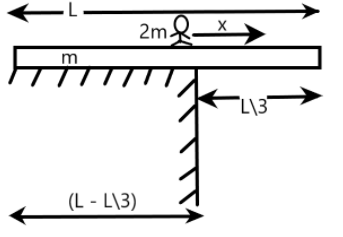
According to the principle of moments, we know that for a system to be balanced at a point, the net torque acting on that point needs to be equal to zero. This suggests that torque on the right ride about a balancing point is equal to the torque on the left side about the balancing point.
Now, let us apply this principle in our case. Let us take the balancing point to be the edge of the table, on which the plank is kept. When the man over the plank starts walking towards the right from the edge of the table, it is obvious that the plank will tend to fall. But before this happens, the man could walk a certain distance and get balanced with the weight of the plank on its left. Clearly, we are required to find this distance. Applying the principle of moments on the plank about the edge of the table, we have
τedge=0⇒τleft=τright
where
τedge is the net torque at the balancing point of the plank, on the edge of the table
τleft is the torque on the left side of the balancing point of the plank
τright is the torque on the right side of the balancing point of the plank
Let this be equation 1.
We know that torque at a point is equal to the product of weight on the given point and the distance between the given point and the point about which the mass tends to rotate.
Therefore, torque on the left side of the balancing point of the plank, τleft is given by
τleft=m×(L−3L)=32Lm
where
τleft is the torque on the left side of the balancing point of the plank
m is the mass of the plank which balances the plank on its left side
L−3L is the length of the plank on the left side of the balancing point of the plank, as shown in the figure
Let this be equation 2.
Similarly, torque on the right side of the balancing point of the plank, τright is given by
τright=2m×(x)=2mx
where
τright is the torque on the right side of the balancing point of the plank
2m is the mass of the person standing on the right side of the plank when the plank is balanced
x is the assumed length of the plank on the right side of the balancing point of the plank, where the person can balance the plank without falling
Let this be equation 3.
Substituting equation 2 and equation 3 in equation 1, we have
τleft=τright⇒32Lm=2mx⇒x=6m2Lm=3L
Therefore, the distance the person can walk on the plank from the edge of the table towards the right, without causing the plank to fall is equal to 3L. This suggests that the person can walk till the right end of the plank, without causing any rotation to the plank.
Hence, the correct answer is option D.
Note:
Students can relate this situation to that of a seesaw. Clearly, for a seesaw to be balanced, product of weight of the child and his/her distance from the center of the seesaw on each side should be equal to the product of weight of another child and his/her distance from the center of the seesaw, on the other side of the seesaw. This is nothing but an application of principle of moments.
