Question

A plank of mass ${m_1} = 8kg$ with a bar of mass ${m_2} = 2kg$ placed on its rough surface, lie on a smooth floor of elevator ascending $\dfrac{g}{4}$. The coefficient of friction is $\mu = \dfrac{1}{5}$ between, ${m_1}$ and ${m_2}$ A horizontal force $F = 30N$ is applied to the plank. Then the acceleration of bar and the plank in the reference frame of elevator are

(A) $3.5m/{s^2},5m/{s^2}$
(B) $5m/{s^2},\dfrac{{50}}{8}m/{s^2}$
(C) $2.5m/{s^2},\dfrac{{25}}{8}m/{s^2}$
(D) $4.5m/{s^2},4.5m/{s^2}$

Answer 1

In the given problem, first we calculate the friction force between ${m_1}$ and ${m_2}$. After then using a free body diagram of ${m_2}$ calculate normal force.After this, calculate acceleration of the plank and bar using the following expression.
$F = ma$
Where
m $=$ mass of body
a $=$ acceleration of body

Complete step by step answer:
Let the frictional force between plank and bar is f and given by the following expression.
$f = \mu N$
Here we can see the normal on bar
N $=$ Pseudo force $+$ weight of the bar
FBD of ${m_2}$

Here
${m_1} = 8kg$
${m_2} = 2kg$
So, $N = 20 + \dfrac{{2g}}{4}$
$N = 20 + \dfrac{{2 \times 10}}{4} = 20 + \dfrac{{20}}{4}$
$\Rightarrow N = 20 + 5$
$\Rightarrow N = 25$ Newton
So, friction force $f = \mu N$
Given that $\mu = \dfrac{1}{5}$
$f = 25 \times \dfrac{1}{5}$
$\Rightarrow f = \dfrac{{25}}{5}$
$\Rightarrow f = 5$ Newton
Acceleration of the bar $=$ force on bar $/$ mass of bar
$=$ frictional force $/$ mass
$\Rightarrow a = \dfrac{5}{2}$
$\therefore a = 2.5m/{s^2}$
Now, we will calculate the acceleration of plank

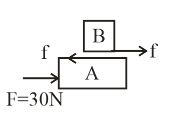
$\Rightarrow 30 - f = m{a_A}$
$\Rightarrow 8 \times {a_A} = 30 - 5$
$\therefore{a_A} = \dfrac{{25}}{8}m/{s^2}$
Hence, the acceleration of bar and plank is $2.5m/{s^2}$ and $\dfrac{{25}}{8}m/{s^2}$ respectively.
Hence option C is the correct answer.

Note: : Many times student may get confused between friction force and normal force.Friction is a force that opposes 2 objects sliding against each other and is a contact force.Normal force is also a contact force and acts perpendicular to the flat surface and in a direction along the flat surface of an object.