Question
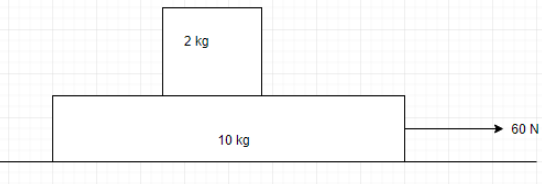
Question: A plank of mass 10kg and a block of mass 2kg are placed on a horizontal plane as shown in the figure...
A plank of mass 10kg and a block of mass 2kg are placed on a horizontal plane as shown in the figure. There is no friction between plane and plank. The coefficient of friction between block and plank is 0.5. A force of 60N is applied on the plank horizontally. In the first 2s the work done by friction on the blocks is?
A. 100 J
B. 100 J
C. 0
D. 200 J
Solution
Between 2 kg block and 10 kg block, there is no friction but between 10 kg and the floor there is friction present. A force acts on a 10 kg block. There can be two possibilities: first that when the force is applied both the block moves with a common acceleration and second could be that only the block on which force is being applied moves, but this can’t be the scenario because it is not mentioned in the question.
Complete step by step answer:
Assuming that both the blocks move with the same acceleration, total mass of the blocks= 12 kg. Coefficient of friction is 0.5. Now when the force of 60 N is applied, both the block moves, so,
F=ma \\\
\Rightarrow 60=12a \\\
\Rightarrow a=\dfrac{60}{12} \\\
\Rightarrow a=5m/{{s}^{2}} \\\
So, the block of mass 2 kg moves with this acceleration, so using Newton’s second law here we get, f=2×5=10N
Also, frictional force acting on the block of mass 10 kg also comes out to be 10 N.Now in first two seconds,
s=\dfrac{a{{t}^{2}}}{2} \\\
\Rightarrow s=\dfrac{5\times {{2}^{2}}}{2} \\\
\Rightarrow s=10m \\\
Now we need to find the work done by the friction,
W=Fs ⇒W=10×10 ∴W=100J
So, the correct option is (A).
Note: Retarding force is that force which opposes the motion of the body on which it is being acted. Remember force is a vector quantity and so its direction is also to be taken into account. Such problems can be briskly solved using Newton’s equations of motions. when more than one force acts on any system then we have to add all the forces vectorially taking into account their directions.
