Question

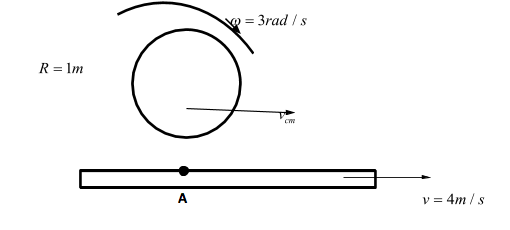
A plank is moving with a velocity of $4~m/sec$. A disc of radius$1~m~$rolls without slipping on it with an angular velocity of $3~rad/sec~$as shown in figure. Find out the velocity of the centre of the disc.

 ![](https://www.vedantu.com/question-sets/ca93af8e-58e2-49d2-bf3a-d8771f23b0cb1196383098301656305.png)

Answer 1

In order to calculate the velocity of the centre of the disc, it can be observed from the question and figure that it is purely rolling the velocity of the point at the bottom will be equal to velocity of the plank. The formula which is to be used is $v=r\omega$.

Complete step-by-step answer:
Since, it is pure rolling the velocity of the point at the bottom will be equal to velocity of plank.
Thus, at point A,
${{V}_{cm}}-RW=\text{ }4$
$={{V}_{cm}}-3=4$
$={{V}_{cm}}=7m/s$

Hence the velocity of center of the disc is $7m/s.$,

Additional Information: Rolling is a type of motion that combines rotation (commonly, of an axially symmetric object) and translation of that object with respect to a surface (either one or the other moves), such that, if ideal conditions exist, the two are in contact with each other without sliding.

Note: While solving this question, we should be careful with the values given in the question. It must be noted while solving, that the formula used here is from rolling motion and also requires basic knowledge of rolling motion. The values given in the question should be kept in the formula carefully. At any instant of time, there will be two velocities. One is the velocity of the centre of mass and another one is the component of linear velocity. The velocity of the centre of mass is ${v_{cm}}$. This corresponds to the translation motion of the object. $v$ is the linear velocity which corresponds to the rotation,
$v = r\omega$.