Question

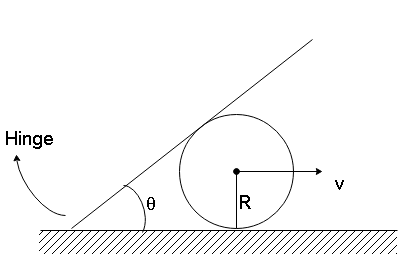
A plank is hinged on a horizontal surface at point A as shown in the figure, find the angular velocity of plank about point A at the instant given in the figure. Solid sphere only translates with velocity $v$ and radius of the sphere is $R$

A) $\dfrac{{2v\sin \dfrac{\theta }{2}}}{R}$
B) $\dfrac{{2v{{\cos }^2}\dfrac{\theta }{2}}}{R}$
C) $\dfrac{{2v{{\sin }^2}\dfrac{\theta }{2}}}{R}$
D) $\dfrac{{2v\sin \theta }}{R}$

Answer 1

The rod is only having translatory motion so the angle of the hinge will be determined by the distance of the rod from the sphere. The angular velocity of the hinge will be equal to the rate of change of the angle formed by the rod.

Complete step by step answer:
In the figure, we can see that the rod is resting on top of the sphere. The sphere translates with velocity $v$ . Since the sphere is moving with constant velocity and has no rotation, it can be considered to be frictionless. Hence the rod will also move smoothly over the sphere.
The angular velocity of the hinge hence will depend on the distance of the sphere from the hinge and the angle formed at a given moment as the rod will always be in contact with the sphere. Let $x$ be the distance of the point of contact of the sphere from the hinge.

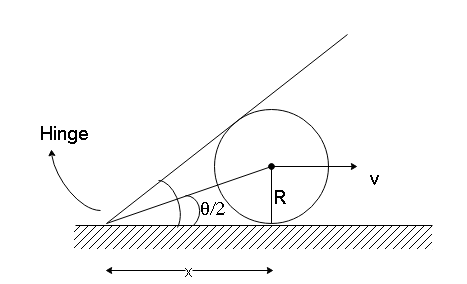
In the above diagram, we can see that
$\tan \dfrac{\theta }{2} = \dfrac{R}{x}$
Which can be simplified to
$x = R\cot \dfrac{\theta }{2}$
Now the velocity of the sphere will be
$v = \dfrac{{dx}}{{dt}}$
$\Rightarrow v = \dfrac{{dx}}{{d\theta }} \times \dfrac{{d\theta }}{{dt}}$
So we can differentiate $x = R\cot \dfrac{\theta }{2}$ and write
$v = R\cos e{c^2}\dfrac{\theta }{2} \times \dfrac{{d\theta }}{{dt}}$
Rearranging the above equation, we can write $\dfrac{{d\theta }}{{dt}} = \dfrac{{2v{{\sin }^2}\dfrac{\theta }{2}}}{R}$ which corresponds to option (C).

Note:
While calculating the derivative of the velocity of the sphere, we should be careful to notice that the angle of the rod will also change with time so it must also be differentiated in accordance with the chain rule of differentiation. Here the sphere will just slide on the rod and won’t rotate which simplifies the position of the rod as a function of time.