Question

A planet moves around the sun in an elliptical orbit with the sun at one of its foci. The physical quantity associated with the motion of the planet that remains constant with time is:
A. velocity
B. centripetal force
C. linear momentum
D. angular momentum

Answer 1

To answer this question we need to have an idea about Kepler's law of planetary motion. There are basically three theorems in Kepler's law. Kepler's law establishes relationships describing the orbital motion. First, we need to mention the laws and the three theorems. Then we can move on to see how the situation mentioned in the question is relatable to the theorems of Kepler's law.

Complete step-by-step solution:
The three theorems of Kepler's law is as follows:
Firstly, the orbit of a planet is an ellipse with the sun at one of the two foci.
Secondly, a line segment that is joining a planet and sun sweeps out equal areas during equal intervals of time.
Lastly, the ratio of the square of an object’s orbital period with the cube of the semi-major of the orbit is the same for all the objects which are orbiting the same primary.
Now moving on to the question.

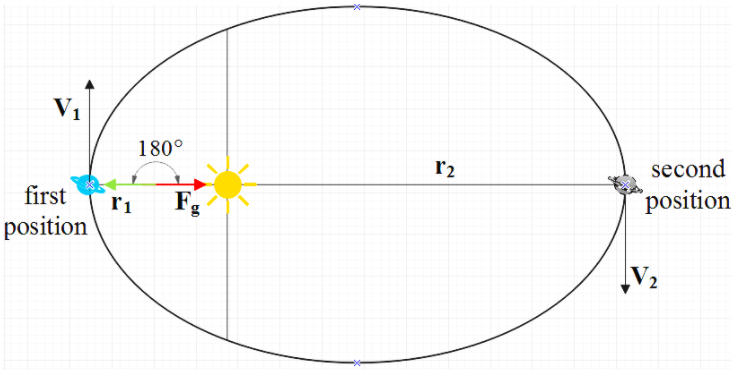
As we know that a planet revolves around the sun in an elliptical orbit under the effect of the gravitational pull of the planet, so therefore we can write the equation of torque as
$\text{ }\\!\\!\tau\\!\\!\text{ = r }\\!\\!\times\\!\\!\text{ F = rFsin180 }\\!\\!{}^\circ\\!\\!\text{ = 0}$
Here, $\text{ }\\!\\!\tau\\!\\!\text{ }$ is the torque acting on the planet
$\text{r}$ is the distance between the planet and the sun.
And $\text{F}$ is the gravitational force due to the sun.
Now, we know that $\tau =\dfrac{dL}{dt}$ .
Where L is the orbital angular momentum.
Then, as $\tau =0$ , $\dfrac{dL}{dt}=0$.
That means, L = a constant.
We can also prove this by taking 2 positions for the planet as shown in the figure.
L is given by the formula, $L=mvr$.
For the first position, $r={{r}_{1}}\text{ and }v={{v}_{1}}$ and for the second position, $r={{r}_{2}}\text{ and } v={{v}_{2}}$ .
But, ${{r}_{1}}\text{ less than }{{r}_{2}}\text{ and }{{v}_{1}}\text{ greater than }{{v}_{2}}$ . So,
$\begin{aligned} & m{{v}_{1}}{{r}_{1}}=m{{v}_{2}}{{r}_{2}} \\\ & \Rightarrow {{L}_{1}}={{L}_{2}} \\\ & \Rightarrow dL=0 \\\ \end{aligned}$
Hence, we can say that the angular momentum is constant.
So, the correct answer is Option D.

Note: So now we know that Kepler's laws are very important as it describes how the planets, even they can be asteroids and comets orbit the sun. It also establishes a relationship to show how the moon orbit around a planet. But they do not apply just to our solar system, they can also be used to describe the orbits of an exoplanet around any star.