Question
Question: A plane wave of wavelength \(\lambda \) is incident at an angle \(\theta \) on a plane mirror. Maxim...
A plane wave of wavelength λ is incident at an angle θ on a plane mirror. Maximum intensity will be observed at P, when
(A) cosθ=2d3λ
(B) secθ−cosθ=4d3λ
(C) cosθ=4dλ
(D) secθ−cosθ=4dλ
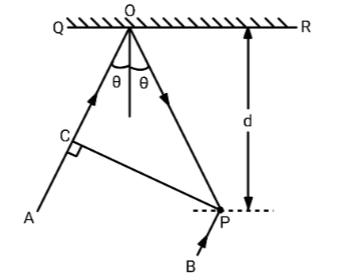
Solution
Here, the first light ray will travel through point A, reflect at point O and then will reach the point P. Another ray of light directly reaches point P. These light rays interfere at point P. For the intensity to be maximum, think of what kind of interference should occur at this point P. One more thing to keep in mind to solve this question is, there is a relationship between the intensity and the amplitude of the electric field of the light, consider this relationship and find the intensity.
Complete step by step solution:
The equation of a light is given by E=E0sin(kx−ωt). Let the equations of the two light rays meeting at point P be given as E=E01sin(kx−ωt) and E=E02sin(kx−ωt+ϕ). The light rays are from a plane wave and therefore they are supposed to be identical. Hence, the amplitude of the two light waves will be equal E01=E02=E0.
When these light rays interfere at point P, by superposition theorem, the resultant of these two waves will be the sum of the two equations. Hence, we have
E=E1+E2 E=E01sin(kx−ωt)+E02sin(kx−ωt+ϕ) E=E0(sin(kx−ωt)+sin(kx−ωt+ϕ))
Now, let us expand and simplify this above resultant E by using trigonometric properties.
Let 1+cosϕ=A and sinϕ=B
E=E0[Asin(kx−ωt)+Bcos(kx−ωt)]
Multiply and divide the equation by A2+B2
{\left( {{E_0}'} \right)^2} = {\left( {\sqrt {{A^2} + {B^2}} } \right)^2}{E_0}^2 \\
{\left( {{E_0}'} \right)^2} = \left( {{A^2} + {B^2}} \right)\left( {{E_0}^2} \right) \\
{\left( {{E_0}'} \right)^2} = \left( {{{\left( {1 + \cos \phi } \right)}^2} + {{\left( {\sin \phi }
\right)}^2}} \right)\left( {{E_0}^2} \right) \\
{\left( {{E_0}'} \right)^2} = {E_0}^2\left( {1 + {{\cos }^2}\phi + 2\cos \phi + {{\sin }^2}\phi }
\right) \\
{\left( {{E_0}'} \right)^2} = 2{E_0}^2\left( {1 + \cos \phi } \right) \\
