Question

A plane wave of monochromatic light falls normally on a uniform thin film of oil which covers a glass plate. The wavelength of source can be varied continuously. Complete destructive interference is observed for $\lambda =5000A{}^\circ$ and $\lambda =7000A{}^\circ$ and for no other wavelength in between. If $\mu$ of oil is 1.3 and that of glass is 1.5, the thickness of the film will be
A. $6.738\times {{10}^{-5}}cm$
B. $5.7\times {{10}^{-5}}cm$
C. $4\times {{10}^{-5}}cm$
D. $2.8\times {{10}^{-5}}cm$

Answer 1

Find the order of each of the given wavelengths. From the figure, find out the path difference between the waves undergoing interference in terms of thickness of the film. Now by applying the condition for destructive interference, find out the thickness of the thin film of oil.

Formula used:
Condition for minima,
$\Delta x=\dfrac{\lambda }{2},\dfrac{3\lambda }{2},\dfrac{5\lambda }{2},...,\left( m+\dfrac{1}{2} \right)\lambda$

Complete step-by-step answer:
We are told that a plane wave of monochromatic light incident normally on a uniform thin film of oil that is covering a glass plate. We are also given the values of two wavelengths for which destructive interference takes place and the refractive index of glass and oil is also given. We have to find the thickness of the film.

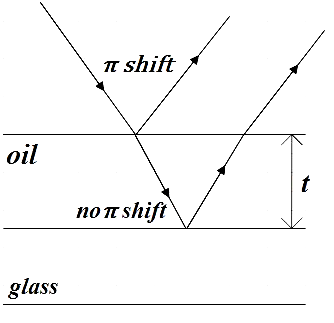
In the question, we are said that no wavelength in between the given wavelengths suffers from destructive interference, so for ${{\lambda }_{1}}\rangle {{\lambda }_{2}}$, if m is the order of ${{\lambda }_{1}}$ then, $m+1$ will be the order of ${{\lambda }_{2}}$.
For normal incidence of the light, we know that the path difference $\left( \Delta x \right)$ will be twice the thickness (t) of the film.
$\Delta x=2t$ ………………… (1)
Since there is a relative phase difference, the condition for destructive interference can be given by,
$\Delta x=\dfrac{\lambda }{2},\dfrac{3\lambda }{2},\dfrac{5\lambda }{2},...,\left( m+\dfrac{1}{2} \right)\lambda$
Where, ‘ $\lambda$ ’ is the wavelength of light in the thin film.
If ${{\lambda }_{1}}$ is the wavelength in air, then wavelength in medium of refractive index n will be,
${{\lambda }_{1n}}=\dfrac{{{\lambda }_{1}}}{n}=\dfrac{7000}{1.3}$
Similarly for ${{\lambda }_{2}}$,
${{\lambda }_{2n}}=\dfrac{{{\lambda }_{2}}}{n}=\dfrac{5000}{1.3}$
For constructive interference,
$\Delta x=\left( m+\dfrac{1}{2} \right){{\lambda }_{1n}}=\left( m+\dfrac{3}{2} \right){{\lambda }_{2n}}$
$\Rightarrow \left( m+\dfrac{1}{2} \right)\dfrac{7000}{1.3}=\left( m+\dfrac{3}{2} \right)\dfrac{5000}{1.3}$
$\Rightarrow 7m+\dfrac{7}{2}=5m+\dfrac{15}{2}$
$\Rightarrow m=2$
But from (1),
$\Delta x=2t=\left( m+\dfrac{1}{2} \right){{\lambda }_{1n}}$
$\Rightarrow 2t=\left( 2+\dfrac{1}{2} \right)\dfrac{7000}{1.3}$
$\Rightarrow t=\dfrac{5\times 7000}{2\times 2\times 1.3}=6730.7A{}^\circ$
$\Rightarrow t=6.730\times {{10}^{-5}}cm$
Therefore, we get the thickness of the thin film as $t=6.730\times {{10}^{-5}}cm$, so option A is the correct answer.
So, the correct answer is “Option A”.

Note: We know that the condition for destructive interference is given for waves with relative $\pi$ shift. $\pi$ -shift happens for light that travels from rarer medium to denser medium. In the figure we see that the first wave only suffers from $\pi$ shift. In the absence of a relative $\pi$ shift, the condition for maxima and minima gets reversed.