Solveeit Logo
Login

Question

Question: A plane progressive wave of frequency 25 Hz, amplitude \(2.5 \times {10^{ - 5}}\)m and initial phase...

A plane progressive wave of frequency 25 Hz, amplitude 2.5×10−52.5 \times {10^{ - 5}}m and initial phase zero moves along the negative x-direction with a velocity of 300 ms−1{\text{m}}{{\text{s}}^{ - 1}}. A and B are two points 6 m apart on the line of propagation of the wave. At any instant the phase difference between A and B is θ\theta . Which of the following is true if the maximum difference between the displacement of the particles at A and B is Δ\Delta ?
(This question has multiple correct options)
A. θ=π B. θ=0 C. Δ=0 D. Δ=5×10−5 m  {\text{A}}{\text{. }}\theta = \pi \\\ {\text{B}}{\text{. }}\theta = 0 \\\ {\text{C}}{\text{. }}\Delta = 0 \\\ {\text{D}}{\text{. }}\Delta = 5 \times {10^{ - 5}}{\text{ m}} \\\

Explanation

Solution

Here, we will proceed by firstly finding out the value corresponding to the wavelength of the given wave. Then, we will finally use the basic relationship between the phase difference and path difference.

Formula used:
v=νλ{\text{v}} = \nu \lambda and θ=2πλ(Δx)\theta = \dfrac{{2\pi }}{\lambda }\left( {\Delta x} \right).

Complete answer:
Given, Frequency of wave ν=25\nu = 25 Hz
Amplitude of wave a = 2.5×10−52.5 \times {10^{ - 5}} m
Initial phase of wave = 0
Velocity of wave v = 300 ms−1{\text{m}}{{\text{s}}^{ - 1}}
Path difference of Distance between points A and B Δx\Delta x = 6 m
Phase difference between A and B = θ\theta

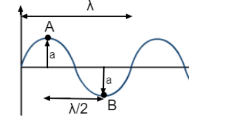
As we know that the velocity of any wave is equal to the product of the frequency of the wave and the wavelength of the wave
v=νλ{\text{v}} = \nu \lambda where v is the velocity of the wave, ν\nu represents the frequency of the wave and λ\lambda represents the wavelength of the wave
⇒λ=vν ⇒λ=30025=12 m  \Rightarrow \lambda = \dfrac{{\text{v}}}{\nu } \\\ \Rightarrow \lambda = \dfrac{{{\text{300}}}}{{25}} = 12{\text{ m}} \\\
The wavelength of the given wave is equal to 12 metres
Also we know that the phase difference between any two points can be written as
θ=2πλ(Δx)\theta = \dfrac{{2\pi }}{\lambda }\left( {\Delta x} \right) where θ\theta denotes the phase difference between the points, λ\lambda represents the wavelength of the wave and Δx\Delta x denotes the path difference between the points
⇒θ=2π12(6)=12π12=π\Rightarrow \theta = \dfrac{{2\pi }}{{12}}\left( 6 \right) = \dfrac{{12\pi }}{{12}} = \pi
So, the phase difference between the points A and B is θ=π\theta = \pi or θ=1800\theta = {180^0}
Let the two points A and B having a phase difference of π\pi or 1800{180^0} are as shown in the figure.
The maximum difference between the displacements of particles at A and B Δ\Delta = 2(Amplitude) = 2×2.5×10−5=5×10−52 \times 2.5 \times {10^{ - 5}} = 5 \times {10^{ - 5}} m

So, the correct answer is “Option A and D”.

Note:
Amplitude of any wave is defined as the distance between the midline and the crest or the trough of the wave. Amplitude usually signifies the amount of the energy transported by the wave. Wavelength of any wave is defined as the distance between two successive crests or troughs of the wave.