Question

A plane progressive wave is represented by the equation$y=0.25\cos (2\pi t-\pi x)$. The equation of a wave with twice the amplitude and half the frequency but travelling in the opposite direction will be
A. $y=0.5\cos (\pi t-\pi x)$
B. $y=0.5\cos (\pi t+\pi x)$
C. $y=0.25\cos (\pi t+2\pi x)$
D. $y=0.5\cos (2\pi t+2\pi x)$

Answer 1

You could begin from the expression for displacement of a plane progressive wave. You could compare this with the given wave’s representation and find out the values of amplitude, frequency and other required quantities from the general expression. As per the given conditions, find out the amplitude and frequency and then you could substitute them in the general expression to get the answer.

Formula used:
Expression for displacement of a plane progressive wave,
$y=A\cos \left( \omega t-\varphi \right)$

Complete answer:
We are given the representation of a plane progressive wave and we are asked to find the equation of displacement of a plane progressive wave whose amplitude is twice the given wave’s amplitude and its frequency is half that of the given wave. It is also said that the new wave to be found is traveling in the opposite direction of the given wave.
As a first step, let us derive the expression for displacement for a progressive wave.

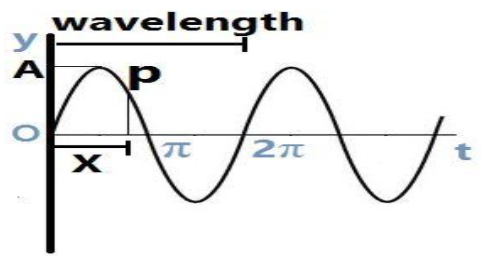
At the point O, the displacement of the progressive wave is given by,
$y=A\cos \omega t$ ……………………… (1)
At the point P, which is at a distance x from O, also lags behind O with a phase difference φ, the displacement is given by,
$y=A\cos \left( \omega t-\varphi \right)$ ………………………… (2)
Where, A is the amplitude.
If ‘$\varphi$’ for $\lambda$ wavelength is$2\pi$ , then, $\varphi$ for unit wavelength is$\dfrac{2\pi }{\lambda }$ . In that case, ‘$\varphi$’ for ‘x’ wavelength will be,
$\varphi =\dfrac{2\pi }{\lambda }x=kx$ ………………………… (3)
Where, $k=\dfrac{2\pi }{\lambda }$ is called the wave number.
We know that angular velocity ω can be given by,
$\omega =\dfrac{2\pi }{T}$
Where, T is the time period of progressive wave.
Also, reciprocal of time period gives us the frequency of the wave. So,
$\omega =2\pi f$ ……………………… (4)
From equations (3) and (4) we can rewrite the displacement in equation (2) as,
$y=A\cos \left( 2\pi ft-kx \right)$ …………………….. (5)
The representation of the given progressive wave is,
$y=0.25\cos (2\pi t-\pi x)$
Comparing this with (5) we get,
Amplitude,
$A=0.25$
$2\pi f=2\pi$
Frequency,
$f=1$
For the wave to be found, amplitude is twice that of the given wave. So, amplitude here is,
$A=2\times 0.25=0.5$
Also, frequency if half that of the given wave,
$f=\dfrac{1}{2}\times 1=\dfrac{1}{2}$
Remember that the direction of this wave is opposite that of the given wave, so, sign should be changed for the ‘kx’ term in the expression. Now, we could substitute the values of A and f in (5) to get,
$y=0.5\cos \left( 2\pi \left( \dfrac{1}{2} \right)t+\pi x \right)$
$y=0.5\cos \left( \pi t+\pi x \right)$
Therefore, the representation of the new wave is,
$y=0.5\cos \left( \pi t+\pi x \right)$

Hence, the answer to the given question option B.

Note:
If you could find the values of frequency, time period, displacement, amplitude and wave number from the simple representation of a plane progressive, you could easily solve this kind of question. Also, try to remember the general representation of a plane progressive wave so that a simple comparison will be all that left for you to do and hence, you could save a lot of time. You should also give importance to the direction.