Question

A plane polarized light entering according to equation x + y + z = constant. angle made with x-axis is

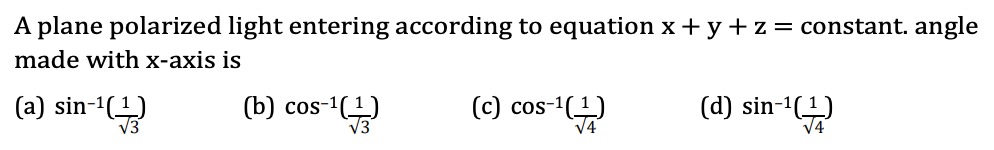
• A. sin$^{-1}$($\frac{1}{\sqrt{3}}$)
• B. cos$^{-1}$($\frac{1}{\sqrt{3}}$)
• C. cos$^{-1}$($\frac{1}{\sqrt{4}}$)
• D. sin$^{-1}$($\frac{1}{\sqrt{4}}$)

Answer 1

Answer: (B)

cos$^{-1}$($\frac{1}{\sqrt{3}}$)

Answer 2

The wavefront is given by

$$x+y+z=\text{constant}.$$

The normal to this plane is $\vec{n}=(1,1,1)$. For plane polarized light, the direction of propagation is along the normal. The angle $\theta$ between $\vec{n}$ and the $x$-axis is given by:

$$\cos\theta=\frac{n_x}{|\vec{n}|}=\frac{1}{\sqrt{1^2+1^2+1^2}}=\frac{1}{\sqrt{3}}.$$

Thus,

$$\theta = \cos^{-1}\left(\frac{1}{\sqrt{3}}\right).$$