Question
Question: A plane metallic sheet is placed with its face parallel to lines of the magnetic induction \( B \) o...
A plane metallic sheet is placed with its face parallel to lines of the magnetic induction B of a uniform field. A particle of mass m and charge q is projected with a velocity v from a distance d from the plane normal to the lines of induction. Then the maximum velocity of projection for which the particle does not hit the plane is,
(A) m2Bqd
(B) mBqd
(C) 2mBqd
(D) d2Bqm
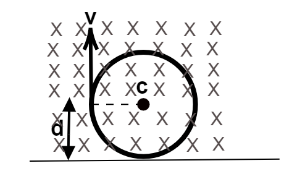
Solution
In the diagram, the bottom line represents the plane metallic sheet that is faced parallel to the magnetic field lines. If a charge is projected upwards, the magnetic force acts on it and deflects it in such a way that it follows a circular path, the radius of this path depends on the velocity of the charged particles, therefore the maximum radius of this circle can be d .
Complete Step by step solution:
It is given in the question that,
The magnetic field strength is, B
The mass of the particle is, m
The charge of the particle is, q
Let the velocity of the particle be v , and the distance from where it is projected be d .
Then this charge will experience a force in a direction perpendicular to both the direction of the magnetic field and the velocity of charge, which will cause it to follow a circular path.
This force is given by,
F=qvBsinθ
Where θ is the angle between the velocity of the particle and the magnetic field lines, since it moves perpendicular to the field, the angle θ is,
θ=2π
We know that, sin2π=1
Putting this value in the formula of force on the charged particle,
F=qvB×1
⇒F=qvB
This force acts as a centripetal force causing the circular motion of the charged particle, as a reaction, a centrifugal force acts on the charge as well,
This centrifugal force is given by,
Fc=rmv2
Where r is the radius of the circle.
We know that to avoid the circle touching the plane, the maximum radius of the circle should be equal to d .
Therefore, equating both forces,
F=Fc
⇒qvB=dmv2
Rearranging this equation, we get-
v=mBdq
Thus, option (B) is the correct answer.
Note:
A charged particle does not experience a force as long as it is on rest, however when it is moved with a velocity, it experiences a magnetic force due to the field around it. A charged particle can move and still not experience magnetic force only when it moves parallel with the magnetic field lines and sinθ becomes zero.
