Question

A plane meets the coordinate axes in A, B, C such that the centroid of DABC is the point (p, q, r). The equation of the plane is –

• A.
• B. $\frac { z } { 2 p } + \frac { y } { 2 q } + \frac { z } { 2 r } = 1$
• C. $\frac { x } { 3 p } + \frac { y } { 3 q } + \frac { z } { 3 r } = 1$
• D.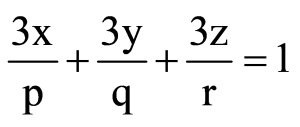

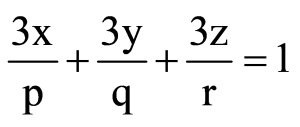
Answer 1

Answer: (C)

$\frac { x } { 3 p } + \frac { y } { 3 q } + \frac { z } { 3 r } = 1$

Answer 2

Equation of the plane be + + = 1

Then coordinates of A, B, C are (a, 0, 0), (0, b, 0), (0, 0, c). So the centroid of the triangle ABC is $\left( \frac { \mathrm { a } } { 3 } , \frac { \mathrm { b } } { 3 } , \frac { \mathrm { c } } { 3 } \right)$

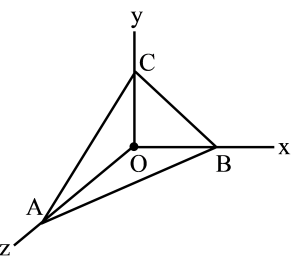
The coordinates of centroid given (p, q, r)

a = 3p b = 3q c = 3r

So the equation of the required plane is

$\frac { x } { 3 p } + \frac { y } { 3 q } + \frac { z } { 3 r }$ = 1