Question

A plane is parallel to two lines whose direction ratios are (1, 0, -1) and (-1, 1, 0) and it contains the point (1, 1, 1). If it cuts the co-ordinate axes at A, B, C then the volume of tetrahedron OABC is ..........c.u., Unit

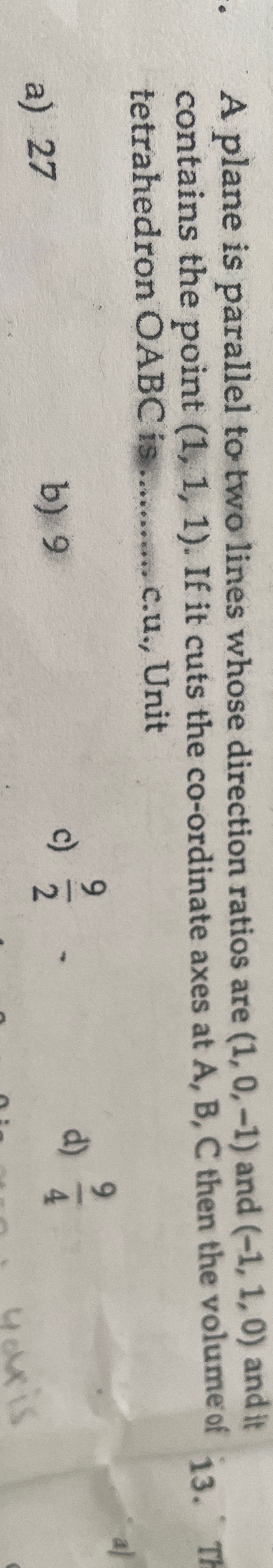
• A. 27
• B. 9
• C. $\frac{9}{2}$
• D. $\frac{9}{4}$

Answer 1

Answer: (C)

$\frac{9}{2}$

Answer 2

Solution:

1. For a plane parallel to the lines with direction ratios (1, 0, –1) and (–1, 1, 0), its normal vector n must satisfy:

   $n \cdot (1,0,-1)=0 \quad\Rightarrow\quad A-C=0\quad\Rightarrow\quad A=C,$

   $n \cdot (-1,1,0)=0 \quad\Rightarrow\quad -A+B=0\quad\Rightarrow\quad B=A.$

   Thus, $n = (A, A, A)$ or simply $(1,1,1)$.

2. The equation of the plane is:

   $x + y + z = d.$

   Since the plane passes through (1, 1, 1):

   $1+1+1 = d \quad\Rightarrow\quad d=3.$

   Hence, the equation is:

   $x+y+z=3.$

3. The intercepts on the axes are:

   $A: (3, 0, 0),\quad B: (0, 3, 0),\quad C: (0, 0, 3).$

4. The volume of tetrahedron OABC is given by:

   $V=\frac{1}{6}\,|OA\cdot OB\cdot OC|=\frac{1}{6}\times3\times3\times3=\frac{27}{6}=\frac{9}{2}.$

Answer:

$\frac{9}{2}$ (Option c)

---

Explanation (minimal):

Normal vector is (1,1,1) ⇒ Plane: x+y+z=3.
Intercepts: (3,0,0), (0,3,0), (0,0,3).
Volume = (1/6)(3×3×3) = 9/2.