Question

A plane flying horizontally at $100\,{\text{m}}{{\text{s}}^{ - 1}}$ releases an object which reaches the ground in $10\,{\text{s}}$. At what angle with the horizontal it hits the ground?
A. $55^\circ$
B. $45^\circ$
C. $60^\circ$
D. $75^\circ$

Answer 1

Use the formula:
$v = u + at$ and find the horizontal and vertical component of velocity.
Use the formula:
$\tan \theta = \,\,\dfrac{{{v_Y}}}{{{v_X}}}$ to find the angle.

Complete step by step solution:
In this given problem, the plane is flying horizontally, whose velocity is $100\,{\text{m}}{{\text{s}}^{ - 1}}$. During the flight, it suddenly drops an object from it. The object does not fall horizontally, rather it will move at an inclination with the horizontal.
Let the angle at which the object falls to the ground be $\theta$.

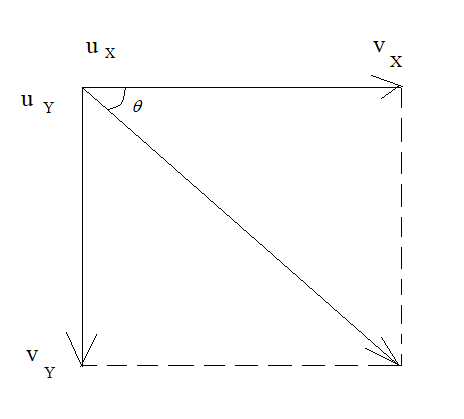
In the figure, the initial and the final velocity of the horizontal motion are indicated along with the initial and final velocity of the vertical motion.
${u_X}$ indicates the initial velocity along the horizontal motion.
${v_X}$ indicates the final velocity along the horizontal motion.
${u_Y}$ indicates the initial velocity along the vertical motion.
${v_Y}$ indicates the final velocity along the vertical motion.

Applying the formula, along the vertical component:
${u_X} = 100\,{\text{m}}{{\text{s}}^{ - 1}}$, ${v_X} = ?$, ${a_X} = 0$ and $t = 10\,{\text{s}}$

$${v_X} = {u_X} + {a_X}t \\\ = 100 + 0 \times 10 \\\ = 100\,{\text{m}}{{\text{s}}^{ - 1}} \\\$$

Applying the formula, along the horizontal component:
${u_Y} = 0\,{\text{m}}{{\text{s}}^{ - 1}}$, ${v_X} = ?$, ${a_X} = 10\,{\text{m}}{{\text{s}}^{ - 2}}$ and $t = 10\,{\text{s}}$

$${v_Y} = {u_Y} + {a_Y}t \\\ = 0 + 10 \times 10 \\\ = 100\,{\text{m}}{{\text{s}}^{ - 1}} \\\$$

The horizontal component of velocity is $100\,{\text{m}}{{\text{s}}^{ - 1}}$ and the vertical component of velocity is $100\,{\text{m}}{{\text{s}}^{ - 1}}$.
To find angle at which the object hits the ground:
Find tangent:

$$\tan \theta = \,\,\dfrac{{{v_Y}}}{{{v_X}}} \\\ \tan \theta = \,\,\dfrac{{100}}{{100}} \\\ \tan \theta = \,\,1 \\\ \theta = \,\,{\tan ^{ - 1}}\left( 1 \right) \\\$$

$\theta = 45^\circ$

The angle at which the object hits the ground is $45^\circ$.

Note: In this problem, you are asked to find the angle at which the object hits the ground. For this, you have to take the vertical and the horizontal component separately. While calculating the horizontal component of velocity, take acceleration due to gravity as zero, as the gravitational pull does not act along the horizontal direction.