Question

A plane flies east of south for 00 km then 400 km north and then 20 degrees north of west for 250 km. What is the magnitude of net displacement? (in km)
A. 335
B. 365
C. 395
D. 345

Answer 1

In this question we have been asked to calculate the magnitude of displacement of a plane. The plane follows a given path. We know that the displacement is a vector quantity. Therefore, we shall be calculating the vector sum of the path followed by the plane. We shall first calculate the vector along both axes. We shall then calculate the net resultant vector.
Formula Used: ${{D}_{net}}=\sqrt{D_{x}^{2}+D_{y}^{2}}$
Where,
D is the displacement

Complete answer:
We have been given that the plane moves flies as shown in the figure below.

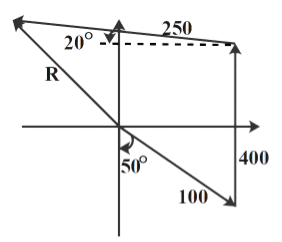
We know that the displacement is a vector quantity, therefore, it has magnitude as well as direction. Since we are asked only magnitude, we shall do the vector addition of the displacement along each axis.
We know that net displacement is given by,
${{D}_{net}}=\sqrt{D_{x}^{2}+D_{y}^{2}}$ …………… (1)
Solving for ${{D}_{x}}$,
${{D}_{x}}={{D}_{{{x}_{1}}}}+{{D}_{{{x}_{2}}}}+{{D}_{{{x}_{3}}}}$
From the diagram we can say that,
${{D}_{x}}=100\cos 50{}^\circ +0-50\cos 20{}^\circ$
On solving,
We get,
${{D}_{x}}=40.8km$ ………… (2)
Now, solving for ${{D}_{y}}$,
${{D}_{y}}=-100\sin 50{}^\circ +400+25\sin 20{}^\circ$
On solving,
We get,
${{D}_{y}}=332km$ …………. (3)
From (1), (2) and (3)
We get,
${{D}_{net}}=\sqrt{{{40.8}^{2}}+{{332}^{2}}}$
On solving we get,
${{D}_{net}}=335km$

Therefore, the correct answer is option A.

Note:
Displacement is a vector quantity that states how far an object is placed from the origin. It is also known as the shortest and straight distance between the initial and the final position. It is a vector quantity. The direction of the resultant vector is calculate using the formula,
$\tan \theta =\dfrac{{{D}_{y}}}{{{D}_{x}}}$