Question
Question: A plane electromagnetic wave propagating through a medium with $\epsilon_r = 8$ and $\mu_r = 2$ has ...
A plane electromagnetic wave propagating through a medium with ϵr=8 and μr=2 has E=21e−3zsin(108t−kz)i^ V/m. [Consider C=3×108 m/s is wave velocity in free space]. Then-
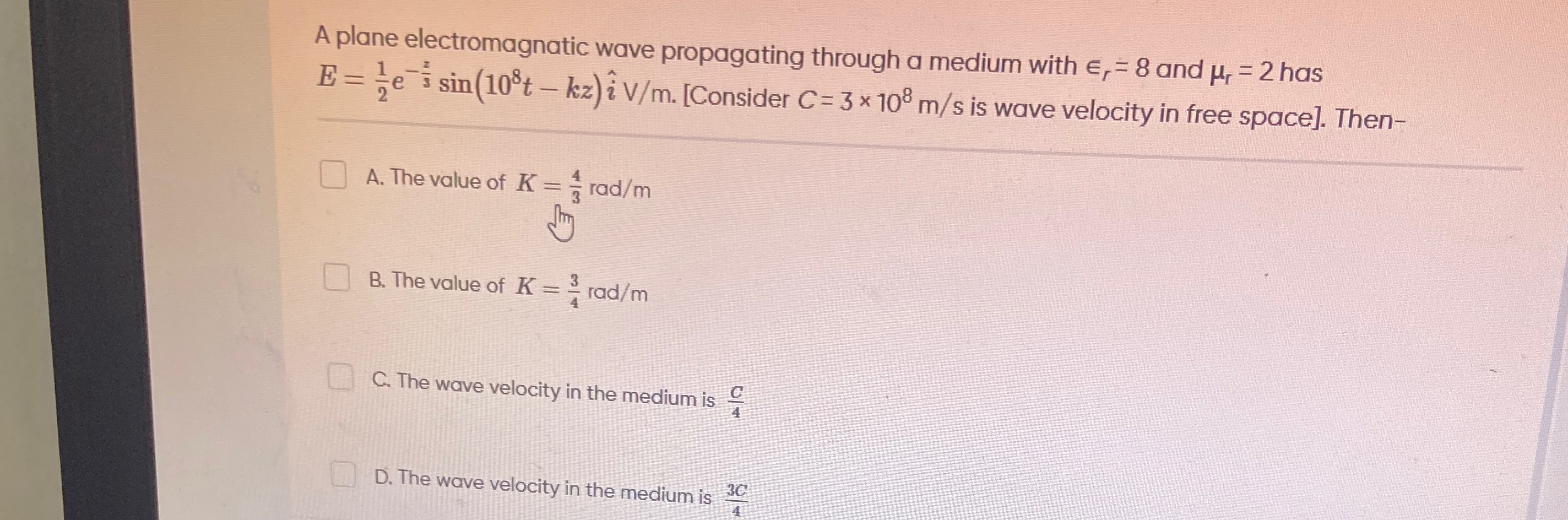
The value of K=34 rad/m
The value of K=43 rad/m
The wave velocity in the medium is 4C
The wave velocity in the medium is 43C
A, C
Solution
The problem asks us to determine the wave number (K) and the wave velocity in a given medium for a plane electromagnetic wave.
-
Calculate the wave velocity (v) in the medium: The velocity of an electromagnetic wave in a medium is given by the formula: v=μrϵrc where c is the speed of light in free space, μr is the relative permeability of the medium, and ϵr is the relative permittivity of the medium.
Given: c=3×108 m/s ϵr=8 μr=2
Substitute these values into the formula: v=2×83×108=163×108=43×108 Since C is used to denote 3×108 m/s in the options: v=4C Therefore, option C is correct.
-
Calculate the wave number (K): From the given electric field equation, E=21e−3zsin(108t−kz)i^ V/m, we can identify the angular frequency (ω) and the wave number (k, which is denoted as K in the options). The angular frequency is ω=108 rad/s. The relationship between angular frequency, wave velocity, and wave number is: K=vω
Substitute the values of ω and the calculated v: K=43×108108=3×108108×4=34 rad/m Therefore, option A is correct.
Both options A and C are correct.
