Question

A plane electromagnetic wave of frequency 50 MHz travels in free space along the x-direction. At a particular point in space $\vec{E} = 7.2\hat{j}$ V/m. At this point, $\vec{B}$ is equal to 1.2x $\times 10^{-8}\hat{k}$ T. Find the value of x.

Answer 1

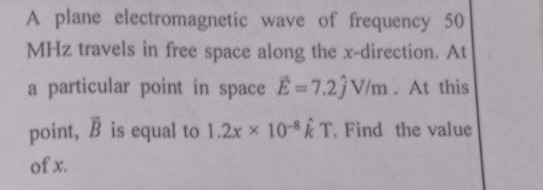
2

Answer 2

The relationship between the magnitudes of the electric field ($E_0$) and magnetic field ($B_0$) in an electromagnetic wave in free space is given by:

$B_0 = \frac{E_0}{c}$

where $c$ is the speed of light in free space, $c = 3 \times 10^8$ m/s.

Given: Magnitude of electric field, $E_0 = 7.2$ V/m. Magnitude of magnetic field, $B_0 = 1.2x \times 10^{-8}$ T.

Substitute these values into the formula:

$1.2x \times 10^{-8} = \frac{7.2}{3 \times 10^8}$

Simplify the right side:

$1.2x \times 10^{-8} = 2.4 \times 10^{-8}$

Divide both sides by $10^{-8}$:

$1.2x = 2.4$

Solve for $x$:

$x = \frac{2.4}{1.2}$

$x = 2$

The directions are consistent as the wave travels along the x-direction ($\hat{i}$), the electric field is along the y-direction ($\hat{j}$), and the magnetic field is along the z-direction ($\hat{k}$). The direction of propagation is given by $\vec{E} \times \vec{B}$, which is $\hat{j} \times \hat{k} = \hat{i}$. This matches the given x-direction of travel.