Question
Question: A planar structure of length \(L\) and width \(W\) is made of two different optical media of refract...
A planar structure of length L and width W is made of two different optical media of refractive indices n1=1.5 and n2=1.44 as shown in the figure. If L≫W, a ray entering from end AB will emerge from end CD only if the total internal reflection condition is met inside the structure. For L=9.6m, if the incident angle θ is varied, the maximum time taken by the ray to exit the plane CD is t×10−9s, where t is __________. [Speed of light c=3×108m/s]
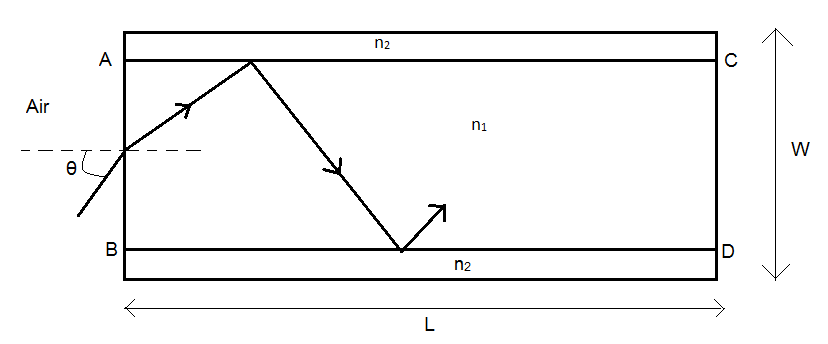
Solution
Hint: We can solve this problem by finding out the critical angle required for total internal reflection and relating it to the distance travelled by the light and the horizontal length covered by it using geometry (after creating a proper diagram) for the first reflection. This can be extended for the whole block. Then using the relation between speed, distance and time, we can get the required time.
Formula used:
θc=sin−1(n1n2)
Speed = TimeDistance
n=vc
Complete step by step answer:
The maximum time will be taken by the light only when it covers the least horizontal distance with each total internal reflection inside the block. This will happen when the angle of incidence for the reflection inside the block is equal to the critical angle (required for total internal reflection).
Therefore, let the angle of incidence for the reflection inside the block be the critical angle θC.
We will draw a diagram to understand it better.
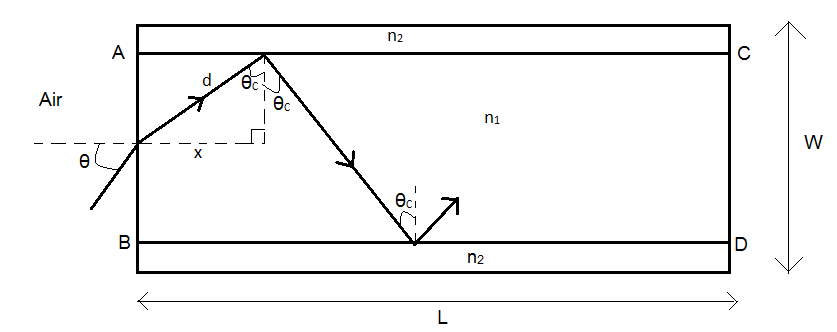
The critical angle θC for total internal reflection when a light ray travelling in medium of refractive index n1 is reflected at the interface of medium of refractive index n2 (where n1>n2) is given by
θC=sin−1n1n2 --(1)
Therefore, now let us analyze the question.
The total horizontal length of the block is L=9.6m.
The outer material of the block has a refractive index of n2=1.44.
The inner material of the block has a refractive index of n1=1.5.
Let the speed of light in the inner material be v.
The speed of light in air is c=3×108m/s.
Now, the refractive index n of a medium is the ratio of the speed of light c in air (or vacuum) to the speed of light v in the medium. Therefore,
n=vc --(2)
Therefore, using (2), we get,
1.5=v3×108
∴v=1.53×108=2×108m/s --(3)
Using (1), we get,
θC=sin−1(1.51.44) --(4)
Also, from the geometry of the figure, we can see
sinθC=dx (∵sin(angle)=hypotenuseperpendicular)
∴θC=sin−1dx --(5)
Equating (4) and (5), we get,
sin−1(1.51.44)=sin−1(dx)
∴1.51.44=dx
∴d=1.441.5x --(6)
Now, for the light to cover the whole horizontal length of the block, that is, L, x=L=9.6m
Putting this in (6), we get,
The total distance D covered by the light as
D=1.441.5×9.6=10m --(7)
Now, Speed = TimeDistance --(8)
Using (8), we get the total maximum time T taken by the light to cover the horizontal length of the block and exit it as
v=TD
∴T=vD
∴T=2×10810=5×10−8=50×10−9s --(9)
Comparing with the question where T=t×10−9s, we get,
50×10−9s=t×10−9s
∴t=50
Hence, the required value of t is 50.
Note: Students should take note that we did not waste time in deriving that the maximum time taken will be in the case when the angle of incidence for total internal reflection inside the block would be for the critical angle. Instead we came to the conclusion by cleverly imagining the path of the light ray and deducing that it will have the least horizontal component (and hence, take the maximum time to cover the horizontal length of the block) when the angle of incidence inside the block is the critical angle. We would have come to this result, even if we would have used calculus and expressions for maxima of a function to derive it. Hence, students should not always resort to mathematical equations but also use logic and analyze the case in the question properly to find out some shorter method or conclusion.
