Question

A pitot tube is inserted in an air flow (at STP) to measure the flow speed. The tube is inserted so that it points upstream into the flow and the pressure sensed by the tube is stagnation pressure The static pressure is measured at the same location in the flow using a wall pressure tap if the pressure difference is 30mm of mercury, determining the flow speed.
A) $80.8m/s$
B) $40m/s$
C) $10.23m/s$
D) None of these

Answer 1

A pitot tube works on principle of bernoulli's theorem basically we convert kinetic energy of flowing fluid into the pressure energy inside the pitot tube.
Bernoulli's equation is $P + \dfrac{1}{2}\rho {v^2} + \rho gh =$ constant

Step by step solution:
Pitot tube is an L shaped tube by which we can find the velocity of flowing fluid as shown in figure

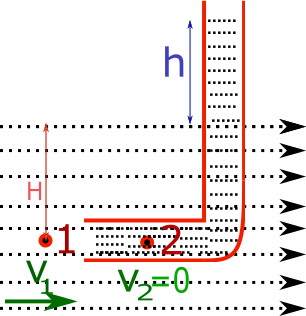
We take 2 point at the same horizontal level point 1 and point 2
Pressure at point 1 is ${P_1}$ and velocity is ${v_1}$ and at point 2 inside the Pitot tube has pressure ${P_2}$ and velocity of fluid ${v_2} = 0$ inside the tube this condition is called stagnation point.
So we apply Bernoulli’s theorem for point 1 and point 2
Energy at point 1= energy at point 2
$\Rightarrow {P_1} + \dfrac{1}{2}\rho {v_1}^2 + \rho gh = {P_2} + \dfrac{1}{2}\rho {v_2}^2 + \rho gh$
As we know point 1 and point 2 is at same horizontal level so $\rho gh$ term will vanish
$\Rightarrow {P_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \dfrac{1}{2}\rho {v_2}^2$
At stagnation point ${v_2} = 0$
$\Rightarrow {P_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2}$
$\Rightarrow \dfrac{1}{2}\rho {v_1}^2 = {P_2} - {P_1}$ .......... (1)
In our question ${P_2} - {P_1}$ is given 30 mm of Hg
Calculate pressure due to 30 mm column of Hg
$\Rightarrow {P_2} - {P_1} = {\rho _{Hg}}gh$
$\Rightarrow {P_2} - {P_1} = 30 \times {10^{ - 3}} \times 13600 \times 10$
Solving this
${P_2} - {P_1} = 3999.67N/{m^2}$
Put this in equation (1)
$\Rightarrow \dfrac{1}{2}\rho {v_1}^2 = 3999.67$
$\Rightarrow {v_1}^2 = \dfrac{{2 \times 3999.67}}{\rho }$
Density of air at STP is $\rho = 1.225kg/{m^3}$
$\Rightarrow {v_1}^2 = \dfrac{{2 \times 3999.67}}{{1.225}}$
Solving this
$\Rightarrow {v_1}^2 = 6530.07$
$\Rightarrow {v_1} = \sqrt {6530.07}$
$\therefore {v_1} = 80.80m/\sec$

Hence option A is correct

Note: The basic pitot tube consists of a tube pointing directly into the fluid flow as this tube contains fluid; a pressure can be measured; the moving fluid is brought to rest (stagnates) as there is no outlet to allow flow to continue; this pressure is the stagnation pressure . This comes due to loss in kinetic energy or dynamic pressure.