Question

A piston of mass $M = 3\,kg$ and radius $R = 4\,cm$ has a whole into which a thin pipe of radius $r = 1\,cm$ is inserted. The piston can enter a cylinder tightly and without friction, and initially it is at the bottom of the cylinder. 750 gm of water is now poured into the pipe so that the piston and pipe are lifted up as shown in the figure. Then,

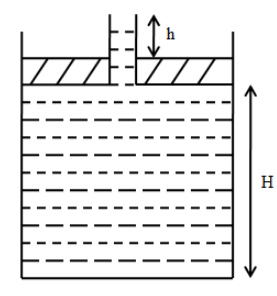
(A) The height H of water in the cylinder is $\dfrac{2}{\pi }$m.
(B) The height H of water in the cylinder is $\dfrac{{11}}{{32\pi }}$m.
(C) The height h of water in the pipe is $\dfrac{2}{\pi }$m.
(D) The height h of water in the pipe is $\dfrac{{11}}{{32\pi }}$m.

Answer 1

For the first we balance the forces acting on the piston. We can express the forces in terms of pressure to determine the height of the liquid column in the pipe. Use the formula for pressure due to air below the depth h in the liquid to determine the pressure exerted by the water in the cylinder on the piston. For the second part, the mass of water poured is equal to the mass of water in the pipe plus the mass of water in the cylinder.

Formula used:
The pressure due to air below the surface of liquid of density $\rho$ is,
$P = {P_0} + \rho gh$
Here, $\rho$ is the density of liquid and g is the acceleration due to gravity.

Complete step by step answer:
We see that after pouring the water into the cylinder, the pipe and cylinder are moved upward and attained equilibrium position. Since the pipe and cylinder are in equilibrium, we can say the force due to atmospheric pressure and the weight of the pipe and cylinder is balanced by the upward thrust of water to the piston. This thrust is due to pressure exerted by the water on the piston.
Therefore, we can write the expression,
${P_0}A + Mg = PA$ …… (1)
Here, ${P_0}$ is the atmospheric pressure, M is the mass piston, g is acceleration due to gravity, P is the pressure exerted by the water below the height h and A is the area of the cylinder.
We can express the pressure P below height h of the water as follows,
$P = {P_0} + \rho gh$ …… (2)
Here, $\rho$ is the density of water and g is the acceleration due to gravity.
We substitute equation (2) in equation (1).
${P_0}A + Mg = \left( {{P_0} + \rho gh} \right)A$
$\Rightarrow {P_0}A + Mg = {P_0}A + \rho ghA$
$\Rightarrow h = \dfrac{M}{{\rho A}}$ …… (3)
We have the area of cylinder is,
$A = \pi \left( {{R^2} - {r^2}} \right)$.
$\Rightarrow A = \pi \left( {{4^2} - {1^2}} \right)$
$\Rightarrow A = 15\pi \,c{m^2} = 15\pi \times {10^{ - 4}}{m^2}$
We substitute 3 kg for M, ${10^3}\,kg/{m^3}$ for $\rho$ and $15\pi \times {10^{ - 4}}{m^2}$ for A in equation (3).
$h = \dfrac{3}{{{{10}^3} \times 15\pi \times {{10}^{ - 4}}}}$
$\Rightarrow h = \dfrac{2}{\pi }m$
We know that mass water poured into the cylinder is equal to the addition of mass of water in the pipe and mass of water in the cylinder.
We have mass of water in the cylinder whose volume is $\pi {R^2}H$ is,
${m_c} = \rho \times \pi {R^2}H$ …… (4)
We have mass of water in the pipe whose volume is $\pi {r^2}h$ is,
${m_p} = \rho \times \pi {r^2}h$ …… (5)
We have given that the total mass poured is 750 gm. Therefore, we can write,
$750 \times {10^{ - 3}} = \rho \times \pi {R^2}H + \rho \times \pi {r^2}h$
$\Rightarrow 0.75 = \pi \rho \left( {{R^2}H + {r^2}h} \right)$
We substitute 4 cm for R, 1 cm for r, ${10^3}\,kg/{m^3}$ for $\rho$ and $\dfrac{2}{\pi }m$ for h in the above equation.
$0.75 = \pi \left( {{{10}^3}} \right)\left( {{{\left( {0.04} \right)}^2}\left( H \right) + {{\left( {0.01} \right)}^2}\left( {\dfrac{2}{\pi }} \right)} \right)$
$\Rightarrow \dfrac{{0.75}}{{\pi \left( {{{10}^3}} \right)}} = \left( {1.6 \times {{10}^{ - 3}}} \right)\left( H \right) + \left( {0.1 \times {{10}^{ - 3}}} \right)\left( {\dfrac{2}{\pi }} \right)$
$\Rightarrow \dfrac{3}{{4\pi }} - \left( {0.1} \right)\left( {\dfrac{2}{\pi }} \right) = \left( {1.6} \right)\left( H \right)$
$\Rightarrow \dfrac{{11}}{{20\pi }} = \left( {1.6} \right)\left( H \right)$
$\therefore H = \dfrac{{11}}{{32\pi }}m$

Therefore, the height of water in the cylinder is $\dfrac{{11}}{{32\pi }}m$.So, the correct answer is option (B) and (C).

Note: The formula, $P = {P_0} + \rho gh$ is applicable only when we want to determine the pressure below the surface of liquid at depth h. The crucial step in this question is to determine the area of the cylinder. For this we have subtracted the area of pipe from the total area of the cylinder. Also, note that in the above figure, the height h is from the surface of the water in the cylinder.