Question

A piston divides a closed gas cylinder into two parts. Initially the piston is kept pressed such that one part has a pressure P and volume 5V and the other part has pressure 8P and volume V. The piston is now left free. Find the new pressures and volumes for the adiabatic and isothermal processes. For a gas $\gamma = 1.5$.

Answer 1

As the piston is free to move on its own, it will find an equilibrium such that the pressure on the right side of it will be equal to pressure on the left side. Adiabatic and isothermal pressure volume relation has to be applied to find new pressure and volume.
Formula used:
For isothermal processes,
PV = constant.
For adiabatic processes,
$PV^{\gamma}$ = constant.

Complete answer:
We are given that part A (say) is at a pressure 8P and volume V, and part B (say) is at pressure P and volume 5V.

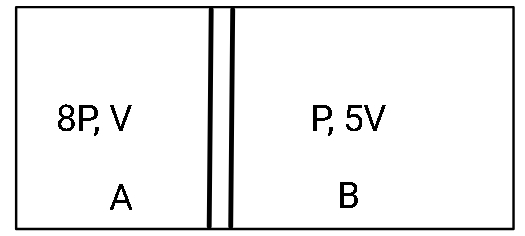
Let us assume the final pressure of the two parts becomes P'. Total volume remains the same so, for part A, we consider new volume as V' and for part B we consider 6V - V'. Now, we treat adiabatic and isothermal processes separately.

1. Adiabatic process: The two parts in the system try to achieve the same pressure by undergoing adiabatic compression or expansion.
For part A,
$8PV^{\gamma} = P' (V')^{\gamma}$.
For part B,
$P(5V)^{\gamma} = P' (6V - V')^{\gamma}$.
If we divide part A equation by part B equation, we get:
$8 \left( \dfrac{1}{5} \right)^{\gamma} = \left( \dfrac{V'}{6V - V'} \right)^{\gamma}$.
Now, $\gamma = 1.5 = \dfrac{3}{2}$, so we take power 2/3 on both sides to get:
$8^{2/3} \left( \dfrac{1}{5} \right)= \dfrac{V'}{6V - V'}$.
$\implies \dfrac{4}{5} = \dfrac{V'}{6V - V'}$
$\implies 4 (6V - V') = 5 V'$
$\implies 24 V = 9 V'$
$\implies V' = \dfrac{8}{3}V$
The new pressure will thus come as:
$8PV^{3/2} = P' \left( \dfrac{8}{3} V \right)^{3/2}$
$\implies P' = \left( \dfrac{3}{2} \right)^{3/2} P$
The volume of the remaining part is:
$6V - \dfrac{8}{3} V = \dfrac{10}{3} V$.

2. Isothermal process: The two parts try to achieve the same pressure by undergoing isothermal expansion or compression.
For part A,
$8PV = P' V'$.
For part B,
$P(5V) = P' (6V - V')$.
If we divide part A equation by part B equation, we get:
${8}{5} = \dfrac{V'}{6V - V'}$.
$\implies 48V - 8V' = 5V'$
$\implies V' = \dfrac{48}{13} V$
The remaining volume is:
$6V - \dfrac{48}{13} V = \dfrac{30}{13} V$.
The pressure can be calculated by using part A expression, it will be:
$8P= \dfrac{48}{13} P'$
$\implies P' = \dfrac{13}{6} P$.
So, for adiabatic process, the new pressure will be $\left( \dfrac{3}{2} \right)^{3/2} P$ and for isothermal process the new pressure will be $\dfrac{13}{6} P$.

So, the correct answer is “Option A”.

Note:
Our system is an isolated system. An isolated system will not exchange heat from the surrounding. The volume of part A was V and of part B was 5V, so we wrote a total of 6V and for part A, we used notation V' this means that the total volume of the two containers minus the volume (final) of part A should give the final volume of part B.