Question

A piston can freely move inside a horizontal cylindrical container closed from both ends. Initially, the piston separates the inside space of the cylinder into two equal parts each of volume ${V_0}$ in the same pressure ${P_0}$ and is always at the same temperature. What work has to be performed to increase isothermally the volume of one part of the gas $\eta$ times compared to that of the other by slowly moving the piston?

Answer 1

Since the problem involves gases in a closed cylinder there is a pressure and a corresponding force associated with it. The equation based on the concept of equilibrium is applied in order to determine the forces exerted by the gases on the piston as well as the force exerted by the agent. The formula for the work done in terms of force and displacement is applied along with the concept of ideal gases and the ideal gas equation.

Complete step by step answer:
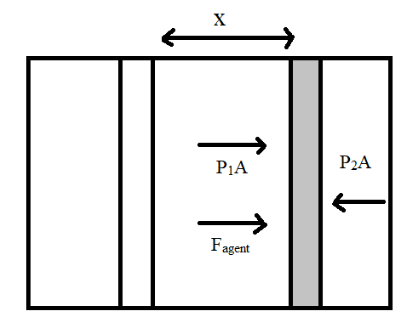
The above problem revolves around the concept of ideal gases inside a closed cylinder. In order to find out the work done in moving the piston we first need to know the concept behind the ideal gases trapped inside a closed cylinder. When a piston is placed inside a cylinder which is closed at both ends then the piston divides the air or the gas inside the cylinder so that there is some amount of gas present on either side of the piston. Hence, the concept of pressure comes into picture because the molecules of the gas particles present on either side of the piston are bound to exert a force on the piston because pressure is said to be the force exerted by a gas per unit area.

Similarly there will be a force that is exerted by the agent on moving the piston to make the volume of one side equal to $\eta$ times the volume of the other side of the piston as given in the question. Hence, to balance out these forces exerted by the gas molecules present in the left side of the piston and the force exerted by the agent will be equivalent to the force exerted by the gas molecules present in the right hand side of the piston as shown in the figure. This is where the concept of equilibrium comes into picture.

Hence by applying the concept of equilibrium we get the equation:
${P_1}A + {F_{agent}} = {P_2}A$
Where, ${P_1}$ indicates the pressure of gas molecules present on the left side of the piston and ${P_2}$ indicates the pressure of gas molecules present on the right hand side of the piston and ${F_{agent}}$ is the force exerted by the agent. Since the same piston is being used the area of the piston is the same everywhere indicated by $A$
By rearranging the terms to make ${F_{agent}}$as the subject we get:
$\Rightarrow {F_{agent}} = {P_2}A - {P_1}A$
By taking out common terms we get:
$\Rightarrow {F_{agent}} = \left( {{P_2} - {P_1}} \right)A$ ---------($1$)

When there is a certain force applied externally on the piston in moving it by a certain amount of displacement $x$ as seen in the diagram, we know that there is some amount of work done in moving the piston. Hence the formula for work done is applied over a small amount of displacement $dx$.
$\Rightarrow dW = {F_{agent}}dx$ --------($2$)
We now substitute equation ($1$) in equation ($2$) to get:
$dW = \left( {{P_2} - {P_1}} \right)A \times dx$
By rearranging the terms we get:
$dW = \left( {{P_2} - {P_1}} \right)\left( {Adx} \right)$

We now apply the formula for volume. Mathematically, we know that the volume is equivalent to the product of area and the height. Here, the height would be the displacement of the piston and hence the volume $V$is said to be equal to the product of area and displacement. Since, $V = A \times dx$, we replace the value in the above equation to get:
$dW = \left( {{P_2} - {P_1}} \right)dV$
Where, $dV$ is the small change in volume due to a small displacement.

The above equation gives the work done for a small amount of displacement resulting in a small change in volume and hence the total work done for the entire change in volume is to be calculated. This is done by integrating the work done over an interval. Hence the above equation becomes:
$\int {dW} = W = \int\limits_0^V {\left( {{P_2} - {P_1}} \right)dV}$ -----------($3$)

We have assumed that the gases inside the cylinder are ideal gases and hence exhibit the properties of ideal gases. Hence, we now apply the ideal gas equation for the gas molecules present inside the cylinder.
$PV = nRT$
Where, $P$ and $V$ are the pressure and volumes respectively. It is mentioned in the question that the temperature is constant, that is, the temperature remains the same at all times and also since the same number of gas molecules that are present on either side of the piston is the same, the number of moles indicated by $n$ is also constant. The universal gas constant is $R$ which is also constant. Hence the above ideal gas equation becomes:
$PV = constant$

When the piston is moved by a certain displacement then there is said to be a change in the pressure and volume values and hence as per the above equation we obtain another equation:
${P_1}{V_1} = {P_2}{V_2}$
This indicates the change in the volumes and pressure after the piston is moved.
Let us now take in consideration the change in the volume. When the piston is moved towards the right hand side of the piston so as to increase the volume of the gas in the left by $\eta$ times the right hand side, we can see that the volume in the left hand side increases and the volume in the right hand side correspondingly decreases.

Since, ${V_0}$ indicates the original volume, the change in the volume on the left hand side will be increased by an amount $Ax$ (with respect to the displacement of the piston toward the right hand side) and change in the volume on the right hand side will be decreased by an amount $Ax$. The amount displaced on the left side will be the same as the amount displaced on the right side.
Hence the equations become:
${P_1}\left( {{V_0} + Ax} \right) = {P_0}{V_0}$
$\Rightarrow {P_2}\left( {{V_0} - Ax} \right) = {P_0}{V_0}$

We have constructed two equations to indicate the change in the pressure and volumes on either side of the piston. The first equation is for the left hand side and the second equation is for the right hand side. By rearranging the terms of the above equations we get:
${P_1} = \dfrac{{{P_0}{V_0}}}{{\left( {{V_0} + Ax} \right)}}$ -------($4$)
$\Rightarrow {P_2} = \dfrac{{{P_0}{V_0}}}{{\left( {{V_0} - Ax} \right)}}$ -------($5$)
We now subtract equation ($5$) from ($4$) to get:
${P_1} - {P_2} = \dfrac{{{P_0}{V_0}}}{{\left( {{V_0} + Ax} \right)}} - \dfrac{{{P_0}{V_0}}}{{\left( {{V_0} - Ax} \right)}}$
We now take the LCM of the equations to get:
${P_1} - {P_2} = \dfrac{{{P_0}{V_0}\left( {{V_0} - Ax} \right) - {P_0}{V_0}\left( {{V_0} + Ax} \right)}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} - Ax} \right)}}$
By taking out common terms we get:
${P_1} - {P_2} = {P_0}{V_0}\left[ {\dfrac{{\left( {{V_0} - Ax} \right) - \left( {{V_0} + Ax} \right)}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} - Ax} \right)}}} \right]$

On further simplification we get:
${P_1} - {P_2} = {P_0}{V_0}\left[ {\dfrac{{{V_0} - Ax - {V_0} - Ax}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} - Ax} \right)}}} \right]$
By cancelling out the common terms we get:
${P_1} - {P_2} = {P_0}{V_0}\left[ {\dfrac{{ - 2Ax}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} - Ax} \right)}}} \right]$
We now reverse the sign of both sides of the equation to get:
${P_2} - {P_1} = {P_0}{V_0}\left[ {\dfrac{{2Ax}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} - Ax} \right)}}} \right]$
$\Rightarrow {P_2} - {P_1} = \dfrac{{{P_0}{V_0}\left( {2Ax} \right)}}{{\left( {{V_0} + Ax} \right)\left( {{V_0} - Ax} \right)}}$
By simplifying further we get:
${P_2} - {P_1} = \dfrac{{{P_0}{V_0}\left( {2Ax} \right)}}{{{V_0}^2 - {{\left( {Ax} \right)}^2}}}$

We know that volume is given as the product of area and volume and hence by substituting $V = Ax$ we get:
${P_2} - {P_1} = \dfrac{{{P_0}{V_0}\left( {2V} \right)}}{{{V_0}^2 - {{\left( {Ax} \right)}^2}}}$
$\Rightarrow {P_2} - {P_1} = \dfrac{{2V{P_0}{V_0}}}{{{V_0}^2 - {{\left( {Ax} \right)}^2}}}$ ----------($6$)
By substituting equation ($6$) in equation ($3$) we get:
$W = \int\limits_0^V {\dfrac{{2V{P_0}{V_0}}}{{{V_0}^2 - {{\left( {Ax} \right)}^2}}}dV}$
We take out the constant terms to get:
$W = {V_0}{P_0}\int\limits_0^V {\dfrac{{2V}}{{{V_0}^2 - {{\left( {Ax} \right)}^2}}}dV}$
$\Rightarrow W = {V_0}{P_0}\int\limits_0^V {\dfrac{{2V}}{{{V_0}^2 - {V^2}}}dV}$
Let us take $x = {V_0}^2 - {V^2}$
Hence, $dx = - 2VdV$ [Differentiation]
$\Rightarrow - dx = 2VdV$

We now substitute this value in the above integral to get:
$\Rightarrow W = {V_0}{P_0}\int\limits_0^V {\dfrac{{ - dx}}{x}}$
$\Rightarrow W = - {V_0}{P_0}\left[ {\log \left( x \right)} \right]_0^V$
We know substitute back the value of $x$ to get:
$W = - {P_0}{V_0}\left[ {\log \left( {{V_0}^2 - {V^2}} \right)} \right]_0^V$
$\Rightarrow W = - {P_0}{V_0}\left[ {\log \left( {{V_0}^2 - {V^2}} \right) - \log \left( {{V_0}^2 - 0} \right)} \right]$
$\Rightarrow W = - {P_0}{V_0}\left[ {\log \left( {{V_0}^2 - {V^2}} \right) - \log \left( {{V_0}^2} \right)} \right]$
Since, $\log a - \log b = \log \dfrac{a}{b}$ we get:
$\Rightarrow W = - {P_0}{V_0}\left[ {\log \dfrac{{\left( {{V_0}^2 - {V^2}} \right)}}{{{V_0}^2}}} \right]$ -----------($7$)

We now determine the relationship between the changes in the volumes of two sides of the piston. As discussed earlier we know that the volume is increased in the left hand side and this is equivalent to $\eta$ times the change in volume on the right hand side that is decreased by the same amount. Hence we obtain the equation:
${V_0} + V = \eta \left( {{V_0} - V} \right)$
By expanding the terms we get:
${V_0} + V = \eta {V_0} - \eta V$
By rearranging the terms we get:
$V + \eta V = \eta {V_0} - {V_0}$

By taking out common terms we get:
$V\left( {1 + \eta } \right) = \left( {\eta - 1} \right){V_0}$
$\Rightarrow V = \dfrac{{\left( {\eta - 1} \right)}}{{\left( {1 + \eta } \right)}}{V_0}$ ----------($8$)
We now substitute equation ($8$) in equation ($7$) to get:
$W = - {P_0}{V_0}\left[ {\log \dfrac{{\left( {{V_0}^2 - {{\left( {\dfrac{{\eta - 1}}{{\eta + 1}}} \right)}^2}{V_0}^2} \right)}}{{{V_0}^2}}} \right]$
By taking out the common terms we get:
$W = - {P_0}{V_0}\left[ {\log \dfrac{{{V_0}^2\left( {1 - {{\left( {\dfrac{{\eta - 1}}{{\eta + 1}}} \right)}^2}} \right)}}{{{V_0}^2}}} \right]$

By cancelling out the common terms we get:
$\Rightarrow W = - {P_0}{V_0}\left[ {\log \left( {1 - {{\left( {\dfrac{{\eta - 1}}{{\eta + 1}}} \right)}^2}} \right)} \right]$
On further simplification we get:
$W = - {P_0}{V_0}\left[ {\log \left( {\dfrac{{{{\left( {\eta + 1} \right)}^2} - {{\left( {\eta - 1} \right)}^2}}}{{{{\left( {\eta + 1} \right)}^2}}}} \right)} \right]$
$\Rightarrow W = - {P_0}{V_0}\left[ {\log \left( {\dfrac{{2\eta + 2\eta }}{{{{\left( {\eta + 1} \right)}^2}}}} \right)} \right]$
$\Rightarrow W = - {P_0}{V_0}\left[ {\log \left( {\dfrac{{4\eta }}{{{{\left( {\eta + 1} \right)}^2}}}} \right)} \right]$
Since, $\log \dfrac{a}{b} = - \log \dfrac{b}{a}$ we get:
$W = {P_0}{V_0}\left[ {\log \left( {\dfrac{{{{\left( {\eta + 1} \right)}^2}}}{{4\eta }}} \right)} \right]$
$\Rightarrow W = {P_0}{V_0}\log \left( {\dfrac{{{{\left( {\eta + 1} \right)}^2}}}{{4\eta }}} \right)$

Hence, this is the work done in increasing the volume isothermally by moving the piston.

Note: A common error which can be made in this problem is that the change in the volume is not considered. The change in the volume from its original volume after moving the piston must be taken into consideration and this change will be the same in both the sides.A point to note is that in reality gases are not ideal in nature and are said to exhibit non ideal behavior.