Question
Question: A pipe of length \(85cm\) is closed from one end. Find the number of possible natural oscillations o...
A pipe of length 85cm is closed from one end. Find the number of possible natural oscillations of the air column in the pipe whose frequencies lie below 1250Hz. The velocity of sound in air is 340m/s.
(A) 6
(B) 4
(C) 12
(D) 8
Solution
To solve this question, we need to use the formula for the frequency of the sound in a pipe which is closed at one end. From there we can find out the values of the possible frequencies.
Formula used: The formula used to solve this question is given by
λ=fv, here λ is the wavelength, v is the velocity, and f is the frequency of a wave.
Complete step-by-step solution:
We know that at the open end of a pipe, an antinode is formed. Also, at the closed end, a node is formed. So for the fundamental frequency, there will be one node and one antinode along the length of the pipe. We know that the distance between the node and the anti node is equal to one fourth of the wavelength. So the length of the pipe is
L=4λ
⇒λ=4L
We know that λ=fv. So we have
f0v=4L
⇒f0=4Lv (1)
According to the question, v=340m/s and L=85cm=0.85m. Putting these above, we get
f0=4×0.85340
On solving we get
f0=100Hz (2)
So the fundamental frequency is equal to 100Hz.
Now, for the first overtone frequency, there will be two nodes and two antinodes, as shown below.
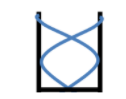
So the length of the pipe in this case is
L=43λ
Substituting λ=fv, we get
L=4f13v
⇒f1=4L3v
From (1)
f1=3f0
Similarly, we can prove that the frequency of the nth overtone is given by
fn=(2n+1)f0
From (2)
fn=(2n+1)100Hz
According to the question, we have to determine the number of oscillations of air below the frequency of 1250Hz. Therefore, we substitute fn=1250Hz above to get
1250=(2n+1)100
⇒2n+1=12.5
On solving we get
n=5.75
So the greatest number of overtone frequencies of oscillations of the air is equal to 5. But there is also natural frequency which is not included in this calculation. So on adding it we get a total of 6 possible oscillations of the air below the given frequency of 1250Hz.
Hence, the correct answer is option A.
Note: We should not forget to include the natural frequency in your final count of the oscillations. This is because the fundamental mode of oscillation is also a valid oscillation of the air column inside the pipe.
