Question

A pipe $ABCD$ of uniform cross-section is bent into three sections, viz. a horizontal section $AB$, a vertical section $BC$ with $C$ below $B$, and a horizontal section $CD$. Liquid flowing through the pipe has speed ${v_1}$ and pressure ${p_1}$ in section $AB$, and speed ${v_2}$ and pressure ${p_2}$ in section $CD$. Determine the relation between ${v_1}$ and ${v_2}$ ; ${p_1}$ and ${p_2}$?
(A) ${v_1} = {v_2}$, ${p_1} = {p_2}$
(B) ${v_1} = {v_2}$, ${p_2} > {p_1}$
(C) ${v_2} > {v_1}$, ${p_2} > {p_1}$
(D) ${v_2} > {v_1}$, ${p_1} = {p_2}$

Answer 1

The relation between the two velocities and pressure can be determined by the help of Bernoulli’s equation in fluid mechanics. By equating the input equation with the output equation, the relation between the two velocities and the two pressures can be determined.

Complete step by step answer:

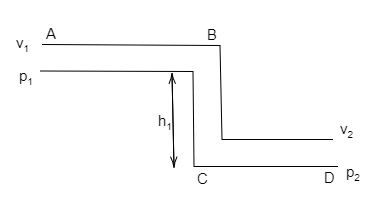
Useful formula:
Bernoulli’s principle,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} + {p_2}$
Where, $\rho$ is the density of the liquid flowing in the tube, $g$ is the acceleration due to gravity, ${h_1}$ is the elevation of the tube $AB$, ${h_2}$ is the elevation of the tube $CD$, ${v_1}$ is the velocity of the liquid flowing in the tube at input, ${v_2}$ is the velocity of the liquid flowing in the tube at output,
${p_1}$ is the pressure of the liquid flowing in the tube at input, ${p_2}$ is the pressure of the liquid flowing in the tube at output.

Complete step by step solution:
By Bernoulli’s principle, the total energy of the fluid flowing in the tube is equal to the sum of the potential energy, kinetic energy and the pressure energy.

By Bernoulli’s equation,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g{h_2} + {p_2}\,................\left( 1 \right)$
Here the fluid is flowing from top to bottom, so the elevation of the tube $CD$ is assumed to be zero, then the above equation is written as,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + \rho g\left( 0 \right) + {p_2}$
On multiplying the terms, then the above is,
$\dfrac{1}{2}\rho {v_1}^2 + \rho g{h_1} + {p_1} = \dfrac{1}{2}\rho {v_2}^2 + {p_2}$
By taking the density outside from the above equation on both sides, then the above equation is written as,
$\rho \left( {\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho }} \right) = \rho \left( {\dfrac{{{v_2}^2}}{2} + \dfrac{{{p_2}}}{\rho }} \right)$
By cancelling the term density on both sides, then the above equation is,
$\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{v_2}^2}}{2} + \dfrac{{{p_2}}}{\rho }$
Here the area of the pipe is constant, then there is no change in velocity, then assume that ${v_1} = {v_2}$, then the above equation is written as,
$\dfrac{{{v_1}^2}}{2} + g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{v_1}^2}}{2} + \dfrac{{{p_2}}}{\rho }$
By cancelling the same velocity terms on both sides, then the above equation is,
$g{h_1} + \dfrac{{{p_1}}}{\rho } = \dfrac{{{p_2}}}{\rho }$
By rearranging the terms for further calculation, then,
$g{h_1} = \dfrac{{{p_2}}}{\rho } - \dfrac{{{p_1}}}{\rho }$
By taking the density common in the denominator,
$g{h_1} = \dfrac{1}{\rho }\left( {{p_2} - {p_1}} \right)$
The above equation is written as,
$\rho g{h_1} = {p_2} - {p_1}$
Here, there is a pressure difference which shows that the pressure ${p_2}$ is greater than the pressure ${p_1}$.
Hence, the option (B) is correct.

Note: If the area of the pipe is increased, then the velocity is decreased and if the area of the pipe is decreased, then the velocity is increased. But in this problem the area of the pipe is constant, then the velocity is constant. And there is some pressure difference between ${p_2}$ and ${p_1}$, so the pressure ${p_2}$ is greater than ${p_1}$.