Question

A pin which is 2 cm long is placed at a distance of 16 cm from a convex lens. Assuming it to be perpendicular to the principal axis, find the position, size and nature of the image if the focal length of the lens is 12 cm.

Answer 1

A convex lens is converging lens i.e., the rays entering the lens will converge to a point upon refraction. So the object must have gotten magnified upon refraction. A positive magnification suggests that the image formed is virtual and erect and a negative magnification suggests that the image is real and inverted. The object is usually placed to the left of the lens.

Formulas used:
->The thin lens equation is given by, $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ where $v$ is the image distance, $u$ is the object distance and $f$ is the focal length of the lens.
->The magnification of a lens is given by, $m = \dfrac{{{h_i}}}{{{h_o}}} = \dfrac{v}{u}$ where ${h_i}$ and ${h_o}$ are the heights of the image and object respectively while $v$ and $u$ are the image distance and the object distance respectively.

Complete step-by-step solution:
->Step 1: List the parameters mentioned in the question and sketch a figure of the setup.

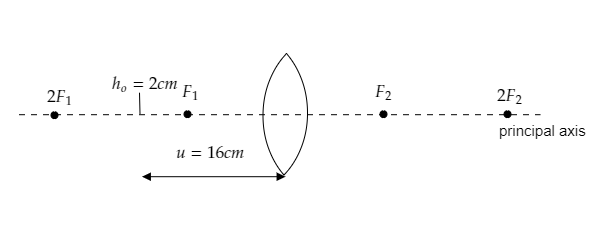
The object distance is given to be $u = 16{\text{cm}}$ and the height of the object is ${h_o} = 2{\text{cm}}$ .
The focal length of the convex lens is given to be $f = 12{\text{cm}}$ .
Let $v$ be the image distance and ${h_i}$ be the height of the image.
->Step 2: Use the lens equation to find the image distance.
The thin lens equation is given by, $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$ or, $\dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u}$ -------- (1)
Substituting for $u = - 16{\text{cm}}$ and $f = 12{\text{cm}}$ in equation (1) we get, $\dfrac{1}{v} = \dfrac{1}{{12}} - \dfrac{1}{{16}}$
$\Rightarrow \dfrac{1}{v} = \dfrac{{4 - 3}}{{48}} = \dfrac{1}{{48}}$
$\Rightarrow v = 48{\text{cm}}$
As the image distance is positive the image formed will be real.
The image is formed at a distance of 48 cm to the right of the convex lens.
->Step 3: Use the relation for the magnification to find the height and nature of the image.
The magnification of the lens is given by, $m = \dfrac{v}{u}$ ------- (2)
Substituting for $v = 48{\text{cm}}$ and $u = - 16{\text{cm}}$ in equation (2) we get, $m = \dfrac{{48}}{{ - 16}} = - 3$
Thus the magnification of the lens is $m = - 3$ . Since the value is negative the image formed will be real and inverted.
Now the magnification of the lens can also be expressed as $m = \dfrac{{{h_i}}}{{{h_o}}}$ ------- (3)
Substituting the values for $m = - 3$ and ${h_o} = 2{\text{cm}}$ in equation (3) we get, $- 3 = \dfrac{{{h_i}}}{2}$
$\Rightarrow {h_i} = - 6{\text{cm}}$
Thus the size of the image will be 6 cm and it is formed below the principal axis.

Note:- The part of the principal axis to the left of the convex lens is considered to be along the negative x-axis and the part to the right of the lens is considered to be along the positive x-axis. So by sign convention, the object distance is negative i.e., $u = - 16{\text{cm}}$. However, the focal length is positive for a convex lens. The values of the object distance and the focal length must be substituted in equation (1) and (2) according to the sign convention.