Question

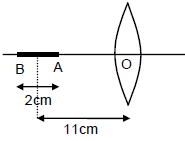
A pin of length $2\,cm$ along the principal axis of a converging lens, the centre being at a distance of $11\,cm$ from the lens. The focal length of the lens is $6\,cm$. Find the size of the image?
A. $3\,cm$
B. $2.4\,cm$
C. $10\,cm$
D. $5\,cm$

Answer 1

Here we have to find the image sizes for both sides of the pin and then find the total size of the image.
Here the object distance is taken as negative since the image will be formed on the other side of the lens. Also, the object distances for points A and B are different.

Complete step by step answer:
Given,
Length of object $= 2\,cm$
Distance of the object from the centre $u = 11\,cm$
Focal length, $f = 6\,cm$

First let us find the image distance for point $A$
\dfrac{1}{f} = \dfrac{1}{{{v_A}}} - \dfrac{1}{{{u_A}}} \\\ \dfrac{1}{6} = \dfrac{1}{{{v_A}}} - \left( { - \dfrac{1}{{10}}} \right) \\\
$\implies {v_A} = 15cm \\\$
Now, let us find the image distance for point B
{f} = \dfrac{1}{{{v_B}}} - \dfrac{1}{{{u_B}}} \\\ \dfrac{1}{6} = \dfrac{1}{{{v_B}}} + \dfrac{1}{{12}} \\\
\implies {v_B} = 12\,cm \\\

So, the length of the image will be $15 - 12 = 3\,cm$

So, the correct answer is “Option A”.

Additional Information:
At the middle, a convex lens is thicker than at sides. A convex lens is a lens that converges. As parallel light rays travel through a convex lens, at one point called the principal focus, the refracted rays converge. The focal length is considered the interval between the principal focus and the centre of the lens.
Although virtual images are often created by diverging lenses, converging lenses are able to generate both actual and virtual images. When the target is positioned less than one focal length from the converging lens, a virtual image is created.
Any incident ray passing parallel to a converging lens’s main axis will refract through the lens and pass on the opposite side of the lens through the focal point.
Any incident ray passing on the way to the lens through the focal point will refract through the lens and travel parallel to the main axis.
In effect, an incident ray that travels through the lens centre would continue in the same direction it had when it reached the lens.

Note:
At the middle, a convex lens is thicker than at sides. A convex lens is a lens that converges. As parallel light rays travel through a convex lens, at one point called the principal focus, the refracted rays converge. The focal length is considered the interval between the principal focus and the centre of the lens.