Question

A pin of length 2.00 cm is placed perpendicular to the principal axis of a converging lens. An inverted image of size 1.00 cm is formed at a distance of 40.0 cm from the pin. Find the focal length of the lens and its distance from the pin.

Answer 1

First we need to draw a ray diagram for the information given in the formula. Then we can make use of the magnification formula and the lens formula to find out the focal length of the lens and the distance of the pin from the lens.

Formula used:
The lens formula is given as
$\dfrac{1}{f} = \dfrac{1}{{\text{v}}} - \dfrac{1}{u}$
where f is used to represent the focal length of the lens, while u and v represent the distance of the object and its image respectively from the lens.
Magnification of the object is given as
$m = \dfrac{{\text{v}}}{{ - u}} = \dfrac{{{h_i}}}{{{h_0}}}$
Here ${h_i}$ is the height of the image while ${h_0}$ is the height of the object.

Complete answer:
The ray diagram for the given question can be drawn in the following way:

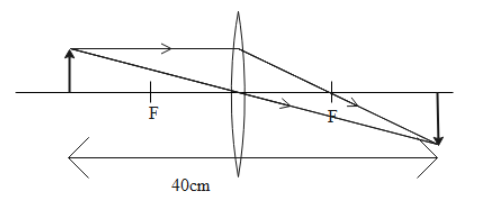
We are given the values of the height of the pin and its image. They are:
${h_0} = 2cm \\\ {h_i} = 1cm \\\$
Therefore, the value of magnification is
$m = \dfrac{{{h_i}}}{{{h_0}}} = \dfrac{1}{2}$
We are also given the distance between the pin and the image to be
$\left( { - u} \right) + v = 40cm$ …(1)
Now we can use the magnification formula in the following way to find out the values of u and v.
$\dfrac{1}{2} = \dfrac{v}{{ - u}} \\\ u = - 2v \\\$
Using this expression in the lens formula, we get
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{v} - \dfrac{1}{{ - 2v}} = \dfrac{1}{v} + \dfrac{1}{{2v}} = \dfrac{3}{{2v}} \\\ \Rightarrow f = \dfrac{{2v}}{3} \\\$
Also, we have
$\- u + v = 40 \\\ \- \left( { - 2v} \right) + v = 40 \\\ 3v = 40 \\\ v = \dfrac{{40}}{3}cm \\\$
Using this value of v in the expression for focal length, we get
$f = \dfrac{{2v}}{3} = \dfrac{{2 \times 40}}{{3 \times 3}} = 8.89cm$
The distance u can be obtained as follows:
$u = - 2v = - 2 \times \dfrac{{40}}{3} = 26.67cm$
Hence, the focal length of the lens is 8.89cm while the distance of the pin from the lens is 26.67cm.

Note:
1. All distances to the left of the lens are taken to be negative while all distances to the right of the lens are taken to be negative.
2. The focal length of a convex lens is positive while that of the concave mirror is negative.