Question

A piece of wood of mass 0.03Kg is dropped from the top of a 100m height building. At the same time, a bullet of mass 0.02Kg is fired vertically upward, with a velocity $100{\text{ m}}{{\text{s}}^{ - 1}}$, from the ground. The bullet gets embedded in the wood. Then the maximum height to which the combined system reaches above the top of the building before falling below is: ($g = 10{\text{ m}}{{\text{s}}^{ - 2}}$).
A. 30 m
B. 10 m
C. 40 m
D. 20 m

Answer 1

Hint: This question is related to inelastic collision i.e. the law of conservation of momentum holds good but the kinetic energy is not conserved. First we need to find the time taken for the particles to collide and speeds of wood and bullet just before collision. Then we need to find the velocity using the law of conservation of momentum. Using this velocity we can now find the maximum height.

Complete step-by-step answer:

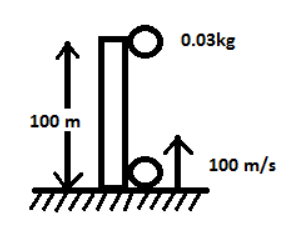
Time taken for the particles to collide,
${\text{t = }}\dfrac{{\text{d}}}{{{{\text{V}}_{{\text{rel}}}}}} = \dfrac{{100}}{{100}} = 1\sec$
Here, d= distance covered
And${{\text{V}}_{{\text{rel}}}}$is the relative velocity
Speed of wood just before collision$= {\text{gt = 10 m/s}}$
Speed of bullet just before collision ${\text{v - gt}} = 100 - 10 = 90{\text{ m/s}}$
Now, conversation of linear momentum just before and after collision
Total momentum before collision = Total momentum after collision
That is, ${m_1}{u_1} + {m_2}{u_2} = {m_1}{v_1} + {m_2}{v_2}$
${m_{total}}{v_c} = {m_b}{v_b} + {m_w}{v_w}$
Where ${m_{total}}$ is combined mass of bullet and wood that is $0.02 + 0.03 = 0.05$,
${v_c}$ is the velocity combination,
${m_b}$ is the mass of bullet,
${v_b}$ is the velocity of bullet,
${m_w}$ is the mass of wooden block
${v_w}$ is the velocity of wooden block
$\Rightarrow \left( {0.03} \right)\left( { - 10} \right) + \left( {0.02} \right)\left( {90} \right) = \left( {0.05} \right){{\text{v}}_c}$
$\Rightarrow - \left( {0.03} \right)\left( {10} \right) + \left( {0.02} \right)\left( {90} \right) = \left( {0.05} \right){{\text{v}}_c}$
$\Rightarrow 150 = 5{{\text{v}}_c}$
$\Rightarrow {{\text{v}}_c}{\text{ = 30 m/s}}$
Maximum height reached by body ${{\text{h}}_{{\text{max}}}}{\text{ = }}\dfrac{{{{\text{v}}^2}}}{{2{\text{g}}}}$
Before collision: $0.03{\text{ kg}} \downarrow 10{\text{ m/s}}$
$0.02{\text{ kg}} \uparrow 90{\text{ m/s}}$
After collision: $30{\text{m/s }} \uparrow {\text{ 0}}{\text{.05kg}}$
$\Rightarrow {{\text{h}}_{{\text{max}}}}{\text{ = }}\dfrac{{30 \times 30}}{{2 \times 10}} = 40{\text{ m}}$
Therefore, the maximum height to which the combined system reaches above the top of the building before falling below is 40 m.

Note: In the above solution, to calculate the time taken for collision we used the distance covered to relative velocity. Instead of that we can also solve by distance covered by piece of wood from certain height in t sec using ${\text{S = ut + }}\dfrac{1}{2}{\text{a}}{{\text{t}}^2}$and then bullet covering distance using the same formula. This total distance now can be equal to the height of the building based on the given question. Solving the equation will give the time taken to collide.