Question

A piece of wire is cut into 5 equal parts. They are the connected parallel. If the equivalent resistance of this combination is ${R}’$, then the ratio $\dfrac{R}{R'}$ is?

Answer 1

Hint: Resistance is proportional to the length of wire and connecting $n$ resistors parallel reduces the resistance $\dfrac{1}{n}$ times.

Formula used: $R = \dfrac{{\rho l}}{A}$ ; $\dfrac{1}{{{R_{eff}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}$

Complete step by step answer:
We know the resistance of a wire is proportional to the length of the wire $\left( {\because R = \dfrac{{\rho l}}{A}} \right)$
Let’s say the total resistance of the wire before cutting was$R$.
When we cut the wire into 5 parts, each one has a length of $\dfrac{l}{5}$ and all other parameters remain unchanged.
So the resistance of each new segment is$\dfrac{R}{5}$.
Connecting them parallel gives a network as shown in fig1.

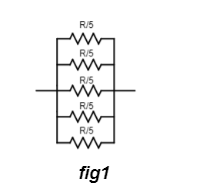
Now since the question asks for The effective resistance of this combination, lets recollect that the effective resistance of a parallel combination of $n$ resistances - ${R_1}$,${R_2}$,${R_3}$, . . . ${R_n}$ is given by: $\dfrac{1}{{{R_{eff}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}$
So if $R'$ is the resistance of this new combination, then:
$\dfrac{1}{{R'}} = \dfrac{1}{{\dfrac{R}{5}}} + \dfrac{1}{{\dfrac{R}{5}}} + \dfrac{1}{{\dfrac{R}{5}}} + \dfrac{1}{{\dfrac{R}{5}}} + \dfrac{1}{{\dfrac{R}{5}}}$
Simplifying this expression a bit gives us:
$\dfrac{1}{{R'}} = \dfrac{5}{{\dfrac{R}{5}}}$
$R' = \dfrac{R}{{25}}$
So the ratio $\dfrac{R}{R'}=25$ , which is the required answer.

Additional Information:
Here the wire was cut and hence the area remained constant. In cases where wire is stretched to a new length, resistance is not proportional to length.
In cases of stretching, since its volume $V$ that is conserved, The Resistance $R$ can be related with length $l$ as $R = \dfrac{{\rho l}}{A} = \dfrac{{\rho l \times l}}{{A \times l}} = \dfrac{{\rho {l^2}}}{V}$.
Thus in case of stretching, the resistance varies as $R \propto {l^2}$

Note: We can answer this question quicker by remembering some special cases in parallel. When we have $n$ equal resistances each of resistance $R$ connected parallel, the effective resistance becomes $\dfrac{R}{n}$.
Here since we have 5 resistances, each of Resistance $\dfrac{R}{5}$
$R' = \dfrac{{\dfrac{R}{5}}}{5} = \dfrac{R}{{25}}$
So $\dfrac{R}{{R'}} = 25$