Question
Question: A piece of uniform wire is made up into two squares with a common side as shown in the figure. Each ...
A piece of uniform wire is made up into two squares with a common side as shown in the figure. Each side has a resistance R. A current enters the rectangular system at one of the corners and leaves through the diagonally opposite corner. Find the current through the common side (I4) in terms of entering current I1.
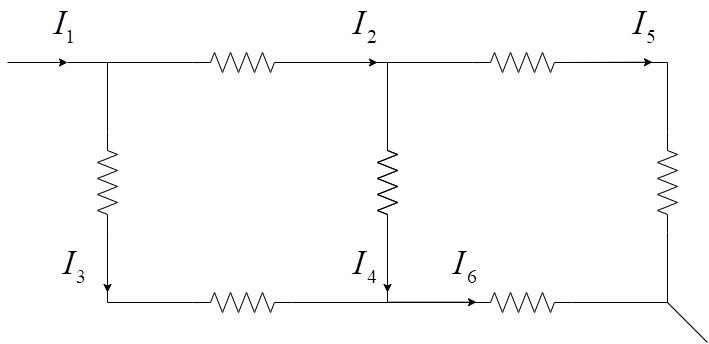
A) 4I1
B) 5I1
C) 7I1
D) 6I1
Solution
There are two electric loops in the question. By applying the Kirchoff’s voltage law, we get two equations. The two equations can only give solutions for only two currents. However, in the question, there are 6 unknown currents. Hence, we have to use the Kirchoff’s current law to derive the relation between the currents and reduce the unknown currents from 6 to 2.
Complete step by step answer:
The relationship among the most important quantities in any electric circuit i.e. electric current and potential difference, required for analysis of any electric circuit is provided by the two Kirchoff’s laws.
Kirchhoff’s 1st law or the Kirchhoff’s current law:
The total current entering a node or a junction of two or more conductors is equal to the total current leaving the node.
Kirchhoff’s 2nd law or the Kirchhoff’s voltage law:
The net voltage drop in a mesh is equal to the emf of the mesh.
Consider the following circuit:
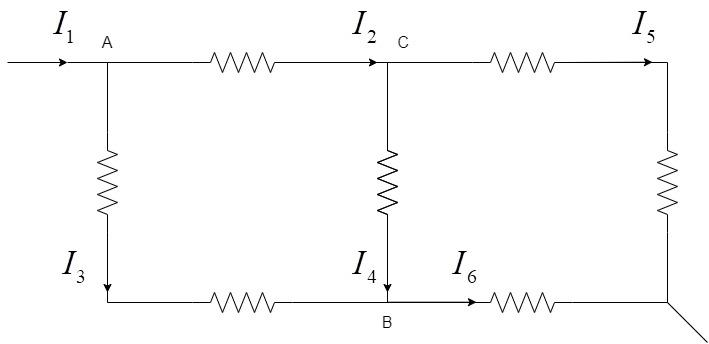 In the question, the currents mentioned are I1 and I4. Hence, every other current must be expressed in terms of these currents. This can be done by applying Kirchhoff's current law to the nodes. Here node refers to the point of intersection of 2 or more conductors. In the given circuit, there are 3 nodes A, B, and C.
In the question, the currents mentioned are I1 and I4. Hence, every other current must be expressed in terms of these currents. This can be done by applying Kirchhoff's current law to the nodes. Here node refers to the point of intersection of 2 or more conductors. In the given circuit, there are 3 nodes A, B, and C.
Applying KCL at the nodes A, B and C –
A: I1=I2+I3
B: I6=I3+I4
C: I2=I4+I5
Applying the Kirchhoff’s voltage laws to the left and the right meshes, we have the following expressions:
Left: I3R+I3R−I4R−I2R=0
Right: I4R+I6R−I5R−I5R=0
Simplifying the above equations, we have –
⇒2I3−I4−I2=0
⇒I4+I6−2I5=0
In these equations, expressing all the currents in terms of I1, I4 and I2 from the equations derived through KCL, we get –
Left: 2I3−I4−I2=0
⇒2(I1−I2)−I4−I2=0
⇒2(I1−I2)−I4−I2=0
⇒2I1−I4−3I2=0
Right: I4+I6−2I5=0
⇒I4+I3+I4−2(I2−I4)
⇒2I4+I1−I2−2I2+2I4=0
⇒I1+4I4−3I2=0
Thus, we have the two equations of the mesh as:
Left: 2I1−I4−3I2=0
Right: I1+4I4−3I2=0
Subtracting the Right equation from the Left equation, we obtain –
⇒2I1−I1−I4−4I4=0
⇒I1−5I4=0
⇒I1=5I4
∴I4=5I1
Hence, the correct option is Option B.
Note: In the question, the current I4 is supposed to be expressed in terms of I1. Along with these currents, the current I2 is considered arbitrarily. The students should understand that there is no fixed rule for taking that and any current i.e., I3 , I5 and I6 can be taken and they will obtain the same result.
