Question

A piece of paper (shown in figure-1) is in the form of a square. Two corners of this square are folded to make it appear like figure-2. Both corners are put together at the centre of the square . If O is taken to be (0, 0), the centre of mass of the new system will be at Figure-1and Figure-2.

$$(A)\;\;\;\left( {\dfrac{{ - a}}{8},0} \right) \\\ (B)\;\;\;\left( {\dfrac{{ - a}}{6},0} \right) \\\ (C)\;\;\;\left( {\dfrac{a}{{12}},0} \right) \\\ (D)\;\;\;\left( {\dfrac{{ - a}}{{12}},0} \right) \\\$$

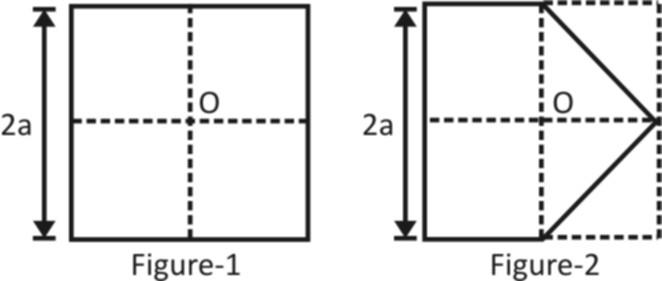
A piece of paper (shown in figure-1) is in the form of a square. Two corners of this square are folded to make it appear like figure-2. Both corners are put together at the centre of the square ‘O’.

Answer 1

Centre of mass of a regular body is the same as their centre. Like the centre of mass of the rectangle lies at the point where its diagonals interest each other.

Complete step by step answer:

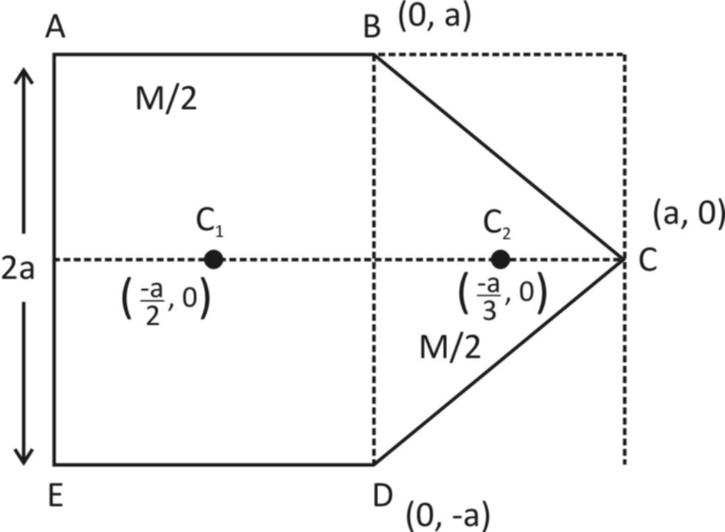
If the total mass of the square sheet is M, then the mass of the ABDE sheet will be $\dfrac{M}{2}$ and that of BCD will also be $\dfrac{M}{2}$.
The centre of mass of ABDE, will be its centre i.e. $G\;\left( {\dfrac{{ - a}}{2},0} \right)$.
Now, BCD is an isosceles triangle.
Its centre of mass will be

$${C_2} = \left( {\dfrac{{o + a + o}}{3},\;\dfrac{{a + o - a}}{3}} \right) \\\ {C_2} = \left( {\dfrac{a}{3},0} \right) \\\$$

Now, centre of mass of whole system will be
Centre of mass along redirection,
${(COM)_x} = \dfrac{{\dfrac{M}{2}\left( {\dfrac{{ - a}}{2}} \right) + \dfrac{M}{2}\;\left( {\dfrac{a}{3}} \right)}}{M} \\\ = \dfrac{{\dfrac{M}{2}\;\left( {\dfrac{{ - a}}{2} + \dfrac{a}{3}} \right)}}{M} = \dfrac{{ - 9}}{{12}} \\\$
Along $y - axis,\;\;(COM){\;_y} = 0$

So, the correct answer is “Option D”.

Note:
Centre of mass of the whole system is calculated by formula
${x_{cm}} = \dfrac{{{m_1}\,{x_1}\, + {m_2}\,{x_2}}}{{{m_1} + {m_2}}} \\\ {y_{cm}} = \dfrac{{{m_1}\,{y_1} + {m_2}\,{y_2}}}{{{m_1} + {m_2}}} \\\$