Question

A piece of iron is heated in a flame. It first becomes dull red then becomes reddish yellow and finally turns to white-hot. The correct explanation for the above observation is possible by using:
A). Stefan’s law
B). Wien’s displacement law
C). Kirchhoff’s law
D). Newton’s law of cooling

Answer 1

Remember that when you are heating a piece of iron you are basically increasing its temperature. And as the temperature increases radiation is emitted at different wavelengths, which is suggestive of the question. Think which law relates to the temperature of the body and the wavelength of light it radiates with the change in temperature. Approaching this from the perspective of blackbody radiation might be the easiest way to arrive at a valid conclusion.

Formula Used:
Wien’s displacement law for blackbody radiation:
$\lambda_{peak} = \dfrac{b}{T}$, where $\lambda_{peak}$ is the peak wavelength in the blackbody spectrum at a temperature $T$, and b is the Wein’s constant $= 2.898 \times 10^{-3}\;m.K = 2898\;\mu m.K$

Complete step-by-step solution:
Let us begin by understanding what blackbody radiation is.
A blackbody is an object that absorbs all radiation incident upon it and re-radiates energy which is characteristic of this system only and is independent of the type of radiation which is incident upon it. The radiation emitted by a blackbody is called blackbody radiation or thermal radiation and is a continuous wavelength (frequency) spectrum that depends only on the body’s temperature. The spectrum is peaked at a characteristic wavelength (frequency) that shifts to lower(higher) wavelengths (frequencies) with increasing temperature.
The figure shows the blackbody spectrum emitted by a blackbody at different temperatures. Each curve represents radiation at a different temperature. Thus, we see that as the temperature increases, the peak shifts towards lower wavelengths, and the light radiated by the blackbody is at the corresponding peak wavelength of the curve at that temperature.

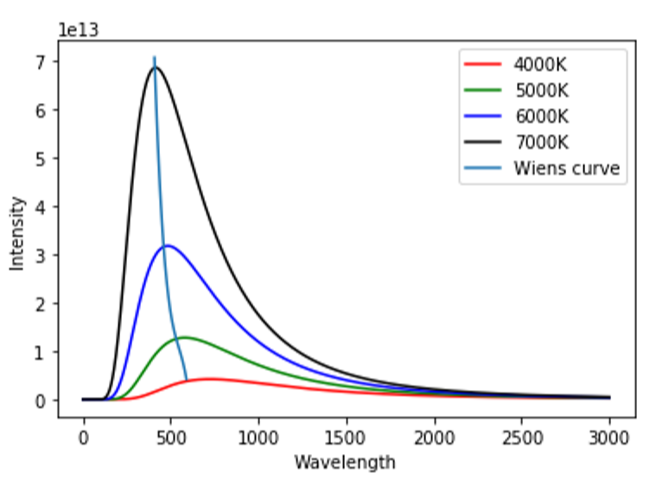
This shift in the peak wavelengths with temperature is given by Wien’s displacement law.
Wien’s displacement law suggests that the black body radiation at different temperatures T will peak at different wavelengths $\lambda_{peak}$ and follow an inverse proportionality. This is given as:
$\lambda_{peak} \propto \dfrac{1}{T} \Rightarrow \lambda_{peak} = \dfrac{b}{T}$.
‘b’ is the proportionality constant, called as the Wien’s displacement constant $= 2.89 \times 10^{-3}\;m.K$
$\Rightarrow \lambda_{peak} T = b$ and $b=constant$
$\Rightarrow \lambda_{peak} T = constant$ which is indicated in the diagram as the line passing through the peak wavelengths at different temperatures. This is called the Wien’s curve.
Thus, with a change in temperature, the peak wavelength gets displaced from its previous position and hence we call this law as Wien’s displacement law.
Now, let us get into the context of the question.
When a piece of iron is heated over a flame, we are basically increasing the temperature of the piece of iron. From Wien’s displacement law, as the temperature increases, the wavelength of light emitted will decrease. From the visible region of the electromagnetic spectrum, we know that in the order of decreasing wavelength we have red, orange, and yellow. This is why, upon heating, the iron piece first becomes dull red then becomes reddish yellow and finally turns to white-hot.
Therefore, we can conclude that this occurrence is attributed to Wien’s displacement law and the correct choice would be B. Wien’s displacement law.

Note: This is also the same reason that lies behind the dimmer switch we get with incandescent light bulbs. As the switch is turned to dim the light, the filament temperature decreases and the distribution of color shifts towards longer wavelengths and the light appears redder, which makes it relatively dimmer.
This principle also justifies the different colors of stars that are observed. Hotter stars appear blue while cooler stars appear red.
Note that the blackbody radiation emitted may have ranged over the entire spectrum and not just the visible region. It is just that we can easily observe radiation that is visible to our naked eye, but hotter temperatures warrant radiation in the UV regions as well. Do not forget that radiation is emitted by every blackbody (including us) at room temperature as well, but this is not visible as it mostly lays in the infrared region of the EM spectrum.