Question

A piece of ice slides down an $45{}^\circ$incline in twice the time it takes to slide down a frictionless $45{}^\circ$ incline. What is the coefficient of friction between the ice and the incline?
(a) $\mu =2\sin \theta$
(b) $\mu =\dfrac{3}{4\cot \theta }$
(c)$\mu =2.5\cot \theta$
(d)$\mu =\dfrac{1}{4\tan \theta }$

Answer 1

For this type of question, we should have knowledge of free body diagrams and should ask about Newton’s Law. Firstly, we will draw a free body diagram for both frictionless as well as surface having friction and for here, we will pull out the equation for forces acting on the body. After this we will calculate length for both types of surfaces. Now, we will equate all the equations and get the value of the coefficient of friction between the ice and the incline.

Complete step by step answer:
Firstly, we will draw the free body diagram for the frictionless surface,

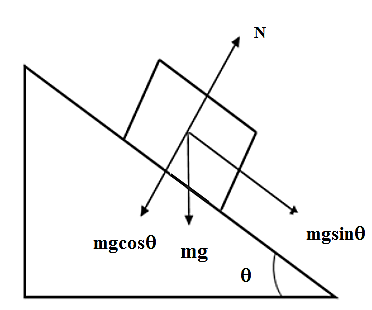
As acceleration is downwards so, from the above figure we can write by applying Newton’s second law as,
$m{{a}_{1}}=mg\sin \theta$
$\therefore {{a}_{1}}=g\sin \theta$ ………………….. (1)
Now, we will draw the free body diagram for the frictional surface,

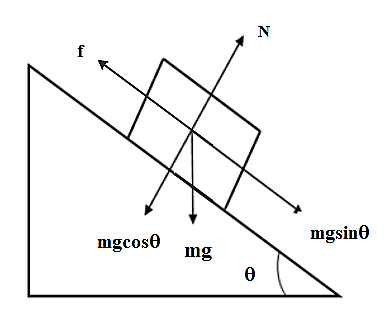
So, from above figure of frictional surface we can write:
$\begin{aligned} & N=mg\cos \theta \\\ & f=\mu N \\\ & \Rightarrow f=\mu mg\cos \theta \\\ \end{aligned}$
Again, by applying Newton’s second law of motion, we can write above equation as:
$m{{a}_{2}}=mg\sin \theta -f$
$\Rightarrow m{{a}_{2}}=mg\sin \theta -\mu mg\cos \theta$
$\Rightarrow {{a}_{2}}=g(sin\theta -\mu \cos \theta )$ …………………………. (2)
Now, we have to calculate the length of inclination for both surfaces:
For frictionless surface,
$\begin{aligned} & l=0+\dfrac{1}{2}{{a}_{1}}{{t}_{1}}^{2} \\\ & \therefore l=\dfrac{1}{2}{{a}_{1}}{{t}_{1}}^{2} \\\ \end{aligned}$ …………………… (3)
For frictional surface,
$\begin{aligned} & l=0+\dfrac{1}{2}{{a}_{2}}{{t}_{2}}^{2} \\\ & \therefore l=\dfrac{1}{2}{{a}_{2}}{{t}_{2}}^{2} \\\ \end{aligned}$ ……………………… (4)
As mentioned in the question the relation between time will be –
${{t}_{2}}=2{{t}_{1}}$ ……………………….. (5)
$\Rightarrow$ Dividing equation (3) and equation (4), we get,
$1=\dfrac{{{a}_{1}}{{t}_{1}}^{2}}{{{a}_{2}}{{t}_{2}}^{2}}$
$\Rightarrow {{(\dfrac{{{t}_{2}}}{{{t}_{1}}})}^{2}}=\dfrac{{{a}_{1}}}{{{a}_{2}}}$
Now we will put the value of acceleration for both the surfaces in above equation –
$\begin{aligned} & \Rightarrow {{(2)}^{2}}=\dfrac{g\sin \theta }{g(sin\theta -\mu cos\theta )} \\\ & \Rightarrow 4(sin\theta -\mu cos\theta )=\sin \theta \\\ & \Rightarrow 3\sin \theta =4\mu \cos \theta \\\ & \Rightarrow \mu =\dfrac{3}{4}\tan \theta \\\ & \therefore \mu =\dfrac{3}{4\cot \theta } \\\ \end{aligned}$
So, the correct answer is “Option b”.

Note: Keep in mind that on a frictionless surface there is no force present to balance the sine component of the mg but on a frictional surface the force present that balances the sine component of the mg acting downward. We must remember Newton’s Laws because while dealing with free body diagrams and force we need to apply it.