Question

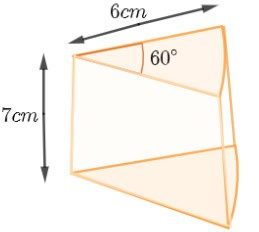
A piece of cheese is cut in the shape of the sector of a circle of radius 6 cm. The thickness of the cheese is 7 cm, then find the curved surface area of the cheese.

(a). $44c{{m}^{2}}$
(b). $40c{{m}^{2}}$
(c). $42c{{m}^{2}}$
(d). $45c{{m}^{2}}$

Answer 1

Hint: If we observe the piece of cheese carefully, we can see that it appears like a sector which is cut from a complete cylinder. We will find the curved surface area of the cheese using the formula, $CSA=\dfrac{\theta }{360}\times 2\pi rh$.

Complete step-by-step answer:
It is given in the question that a cheese is cut in the shape of a sector of a circle of radius 6 cm and thickness 7 cm. We are asked to find the curved surface area of that cheese.

Now, if we observe the cut portion, then it looks like a sector cut from a complete cylinder. We can say that it is a cut piece of a cylinder having a sector of 60˚. Now, we know that the curved surface area of a cylinder is given by the formula, $CSA=2\pi rh$. So, by using this formula, we can say that the curved surface area of the cheese is given by the formula, $CSA=\dfrac{\theta }{360}\times 2\pi rh$ where, $\theta ={{60}^{\circ }}$, $\pi =\dfrac{22}{7}$, r = 6 cm and h = 7 cm. On substituting all these values in the formula, we get,
Curved surface area of the cheese = $\dfrac{60}{360}\times 2\times \dfrac{22}{7}\times 6\times 7$
$\begin{aligned} & =\dfrac{1}{6}\times \dfrac{44}{7}\times 42 \\\ & =44c{{m}^{2}} \\\ \end{aligned}$
Therefore, we get the curved surface area of the cheese as $44c{{m}^{2}}$.
Thus, option (a) is the correct answer.

Note: Students can try to find out the curved surface area by adding the areas of all the faces individually and they can assume all the three faces as rectangle, but one of the face of the cheese is not a rectangle as it is slightly tilted, thus this method is not recommended to solve this question.