Question

A physical balance has its two arms of unequal length. A body weighs 18kg if kept in one pan and weighs 8kg if kept in the other. What is the true weight of the body?
A) 13kg
B) 12kg
C) 10kg
D) 16kg

Answer 1

We need to find the dependence of the length of the arms of the physical balance in giving a true account of the masses kept on its pans. We can relate the parameters and eventually find the true weight of the body by comparing situations.

Complete answer:
We know that a physical balance works on the principle that the product of force (or the weight) and length on an arm equals the same on the other arm of the balance, i.e., the torque should be equal on both arms. When this condition is met, both the arms align horizontally.

  ![](https://www.vedantu.com/question-sets/64c6fd8b-ec4d-438c-b800-efe14545f60f268003545450326099.png)   

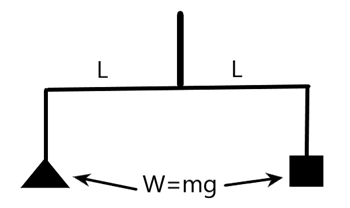
i.e., from the above figure we can say that, if two of the arms are equal then, the weight on both the pans will be equal. It is given by –

& {{\tau }_{1}}={{W}_{1}}\times {{L}_{1}} \\\ & {{\tau }_{2}}={{W}_{2}}\times {{L}_{2}} \\\ & \text{but,} \\\ & {{\tau }_{1}}={{\tau }_{2}} \\\ & \text{and,} \\\ & {{\text{L}}_{1}}={{L}_{2}} \\\ & \Rightarrow {{W}_{1}}={{W}_{2}} \\\ \end{aligned}$$ Now, let us consider the situation in which one of the arms is longer than the other. We will see that in this situation the weights shown on the scale will not be equal. In the below figure, we can see that the right arm is shorter than the left, the torque equations will be – $$\begin{aligned} & {{\tau }_{1}}=W\times L \\\ & {{\tau }_{2}}=W'\times L' \\\ & \text{but,} \\\ & {{\tau }_{1}}={{\tau }_{2}} \\\ & \Rightarrow \dfrac{W}{W'}=\dfrac{L'}{L}\text{ --(1)} \\\ \end{aligned}$$ 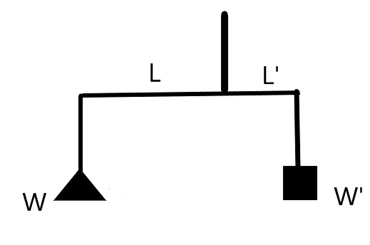 Let us now consider the two given situations when the body and the standard weights are switched positions. CASE I: The right pan has the body which shows the weight as 18kg. Now applying the (1) gives – $$\dfrac{W}{180N}=\dfrac{L'}{L}\text{ --(2)}$$ CASE II: The left pan has the body which now shows as 8kg. 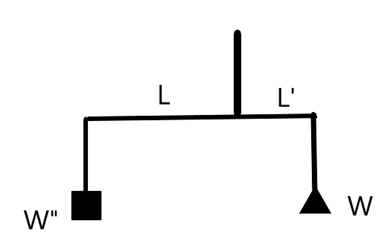 Applying the (1) again for this gives – $$\dfrac{80N}{W}=\dfrac{L'}{L}\text{ --(3)}$$ Now, we can equate (2) and (3) to get the required weight as – $$\begin{aligned} & \Rightarrow \dfrac{80N}{W}=\dfrac{W}{180N} \\\ & \Rightarrow {{W}^{2}}=14400 \\\ & \Rightarrow W=120N \\\ \end{aligned}$$ Therefore, we get the true mass of the body to be 12kg. **So, the correct answer is “Option B”.** **Note:** We should understand that the torque acting on the center rod of the physical balance is responsible for the swinging of masses at the ends. We need to balance this torque such that it cancels out due to equal and opposite forces at either ends of the balance.